Оглавление:
Задание: Нахождение асимптот трафика функции.
Цель: формирование умения находить асимптоты графика функции.
Задание для самостоятельной внеаудиторной работы:
17.1 .Запомните основные виды асимптот графика функции. Проанализируйте, в каких случаях график функции имеет вертикальную асимптоту, в каких — горизонтальную или наклонную.
17.2. Детально изучите и постарайтесь освоить алгоритм, позволяющий находить асимптоты графика функции.
17.3. Найдите асимптоты графика функции:
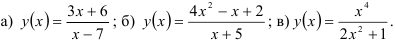
17.4. Найдите асимптоты графика функции:
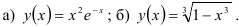
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Поиск асимптот является одним из важных этапов построения графиков функций.
Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная.
- Прямая
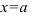называется вертикальной асимптотой функции 
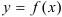, если 
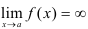. - Прямая
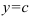называется горизонтальной асимптотой функции 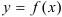, если 
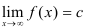. - Прямая
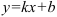называется наклонной асимптотой функции 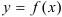, если 
.
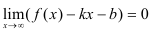На чертеже асимптоты принято обозначать пунктирными линиями.
Рассмотрим следующий искусственно составленный график функции (рис.1), на примере которого хорошо видны все виды асимптот:
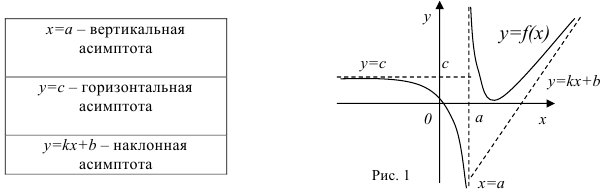
Горизонтальные и наклонные асимптоты рассматриваются только при условии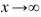 
. Иногда их различают на горизонтальные и наклонные асимптоты при 
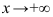и 
.
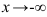Для поиска асимптот удобно использовать следующий алгоритм:
1. Для поиска вертикальных асимптот находим точки, не принадлежащие области определения (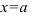) и проверяем следующее условие: если 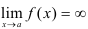, то 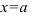— вертикальная асимптота.
Вертикальных асимптот может быть одна, несколько или не быть совсем.
2. Для поиска горизонтальных асимптот находим .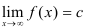
- Если
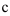— число, то 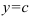— горизонтальная асимптота; - Если 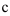— бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим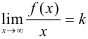 
.
- Если
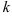— число, отличное от 0, то находим 
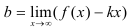. Тогда 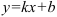— наклонная асимптота; - Если 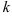— бесконечность, то наклонных асимптот нет.
Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем — их нет.
Рассмотрим примеры нахождения асимптот функции:
Пример 1.
Найдите асимптоты графика функции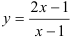 
.
Решение:
1. Найдем область определения функции: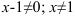 
.
Проверим, является ли прямая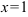 
вертикальной асимптотой. Для этого вычислим предел функции 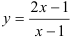в точке 
.
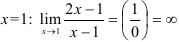Получили, что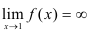 
, следовательно, 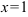— вертикальная асимптота.
2. Для поиска горизонтальных асимптот находим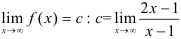 
.
Поскольку в пределе фигурирует неопределенность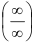 
, воспользуемся правилом Лопиталя: 
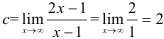. Т.к. 
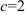(число), то 
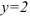— горизонтальная асимптота.
Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.
Таким образом, данная функция имеет вертикальную асимптоту 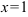и горизонтальную асимптоту .
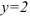Ответ: график функции 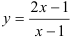имеет вертикальную асимптоту 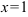и горизонтальную асимптоту .
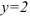Пример 2.
Найдите асимптоты графика функции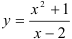 
.
Решение:
1. Найдем область определения функции: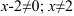 
.
Проверим, является ли прямая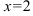 
вертикальной асимптотой. Для этого вычислим предел функции 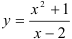в точке 
.
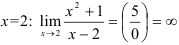Получили, что 
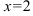, следовательно, — вертикальная асимптота.
2. Для поиска горизонтальных асимптот находим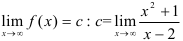 
.
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: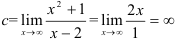 
. Т.к. 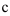— бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим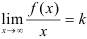 
:
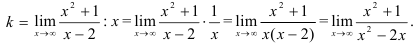
Получили неопределенность вида , воспользуемся правилом Лопиталя:
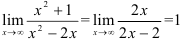. Итак, 
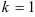. Найдем 
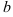по формуле: 
.
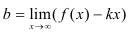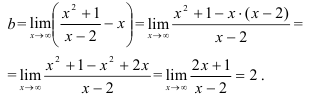
Получили, что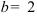 
. Тогда 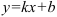— наклонная асимптота. В нашем случае она имеет вид: 
.
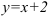Таким образом, данная функция имеет вертикальную асимптоту 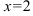и наклонную асимптоту .
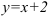Ответ: график функции 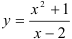имеет вертикальную асимптоту 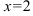и наклонную асимптоту .
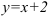На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
