Задание: Действия над комплексными числами в показательной форме.
Цель: формирование умения выполнять операции над комплексными числами в показательной форме.
Задание для самостоятельной внеаудиторной работы:
53.1. Выучите, какой вид имеет показательная форма комплексного числа. Разберите, как выполнить умножение, деление, возведение в степень и извлечение корня из комплексных чисел в показательной форме.
53.2. Закончите высказывания:
а) 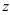 = … — показательная форма комплексного числа, где
= … — показательная форма комплексного числа, где 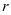 — …,
— …, 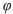 — ….
— ….
б) заполните таблицу по технике действий над комплексными числами в показательной форме:
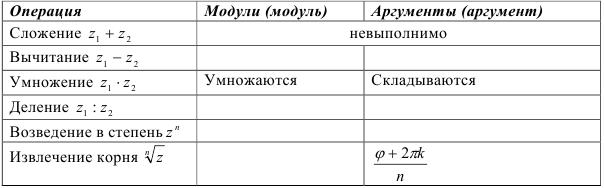
в) Корень 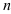 -й степени из числа
-й степени из числа 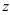 имеет ровно … значений.
имеет ровно … значений.
53.3. Заполните таблицу и постройте на одном чертеже векторы, соответствующие заданным комплексным числам:


53.4. Заданы числа 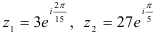 . Выполните указанные действия над комплексными числами в показательной форме:
. Выполните указанные действия над комплексными числами в показательной форме:
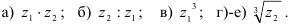

Символ 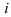 , хотя и был предложен … (задание 52.4), вошел во всеобщее употребление благодаря другому великому математику. Именно он в 1831 году предложил используемое нами по сей день название таких чисел -“комплексные числа”. Слово «комплекс» (от латинского
, хотя и был предложен … (задание 52.4), вошел во всеобщее употребление благодаря другому великому математику. Именно он в 1831 году предложил используемое нами по сей день название таких чисел -“комплексные числа”. Слово «комплекс» (от латинского 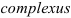 ) означает связь, сочетание, совокупность понятий, предметов, явлений, образующих единое целое.
) означает связь, сочетание, совокупность понятий, предметов, явлений, образующих единое целое.
В начале XIX века было получено также геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган
и наш великий математик независимо друг от друга предложили изображать комплексное число точкой на координатной плоскости.
Выполнив задание 53.4 и заменив получившиеся ответы буквами из таблицы. Вы узнаете (или вспомните) фамилию этого великого математика.
Имя и фамилия математика, предложившего современное название комплексных чисел:

Карта ответов:

53.5. Решите систему линейных уравнений: 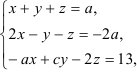 где
где 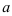 и
и  можно получить, выполнив преобразования:
можно получить, выполнив преобразования: 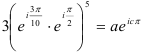 .
.
Методические указания по выполнению работы:
По формуле Эйлера 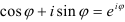 .
.
Тогда 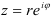 — показательная форма комплексного числа, где
— показательная форма комплексного числа, где 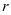 — модуль,
— модуль, 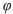 — аргумент комплексного числа.
— аргумент комплексного числа.
Действия над комплексными числами в показательной форме (аналогичны действиям в тригонометрической форме).
Пусть 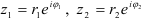 . Над ними выполнимы следующие операции:
. Над ними выполнимы следующие операции:
1. Умножение: 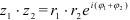 (5). При умножении комплексных чисел в показательной форме их модули перемножаются, а аргументы складываются.
(5). При умножении комплексных чисел в показательной форме их модули перемножаются, а аргументы складываются.
2. Деление: 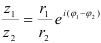 (6). При делении комплексных чисел в показательной форме их модули делятся, а аргументы вычитаются.
(6). При делении комплексных чисел в показательной форме их модули делятся, а аргументы вычитаются.
3. Возведение в степень: 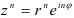 (7). При возведении в степень комплексного числа в показательной форме модуль числа нужно возвести в
(7). При возведении в степень комплексного числа в показательной форме модуль числа нужно возвести в 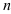 -ю степень, а аргумент умножить на
-ю степень, а аргумент умножить на 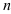 .
.
4. Извлечение корня 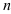 -й степени:
-й степени: 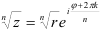 (8), где
(8), где 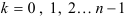 принимает ровно
принимает ровно 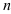 значений.
значений.
Рассмотрим на примерах операции над комплексными числами в показательной форме.
Пример 1.
Для комплексных чисел 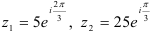 найдите:
найдите: 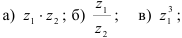
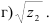
Решение:
а) Согласно формуле (5) получим 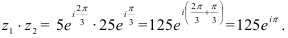
б) Используя формулу (6), находим 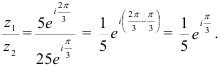
в) Применяя формулу (7), находим 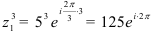 .
.
г) Извлечем квадратный корень из 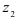 по формуле (8):
по формуле (8): 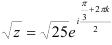 , где параметр
, где параметр 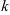 будет принимать значения 0 и 1 (корней 2-й степени из числа существует ровно 2:
будет принимать значения 0 и 1 (корней 2-й степени из числа существует ровно 2: 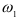 и
и 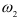 ).
).
При 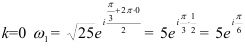 .
.
При 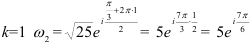 .
.
Ответ: 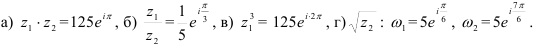
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

