Оглавление:
Сначала идёт подробная теория и потом контрольная работа с решением по каждой теме.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Линейное программирование
Во многих ситуациях, встречающихся в промышленности, сельском хозяйстве, экономической деятельности и т.д., задача оптимизации плана некоторых экономико-производственных действий может быть записана в виде линейных уравнений и неравенств с линейным же, относительно искомых, определяющих этот план, переменных целевой функцией. К задачам этого же вида сводятся очень многие задачи оптимизации и принятия решений из некоторых других самостоятельных направлений прикладной математики.
Возможно эта страница вам будет полезна:
| Предмет математическое программирование |
Соответственно возникает потребность в математической теории, позволяющей решать такие задачи. Такая теория существует и называется линейным программированием. Данное название возникло в 30-е годы, когда представления о программировании на компьютере ещё не существовало. Под программированием фактически подразумевается планирование. Однако, этот термин уже укоренился, и не только в линейном случае. Имеются так же и такие названия математических теорий решения задач оптимизации, как нелинейное программирование и динамическое программирование.
В общем виде задача линейного программирования (ЛП) заключается в отыскании таких неотрицательных чисел 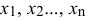 которые максимизируют (минимизируют) линейную функцию:
которые максимизируют (минимизируют) линейную функцию:
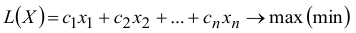
при условии выполнения системы неравенств:
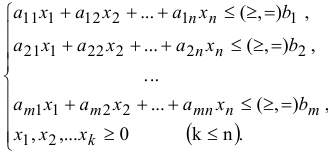
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональность означает, что вклад каждой переменной в целевую функцию (ЦФ) и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если продавая какой либо товар в общем случае по одной цене рублей, фирма будет делать скидку при определенном уровне закупки, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной. Т.е. в разных ситуациях одна единица товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
При решении контрольных работ линейного программирования целесообразно бывает введение следующих определений:
Допустимое решение — это совокупность чисел (план)
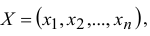
удовлетворяющих ограничениям исходной задачи.
Оптимальное решение — это план, при котором ЦФ принимает свое максимальное (минимальное) значение.
Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических соотношений, необходимо четко разобраться с экономической ситуацией, описанной в условии.
Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1) Что является искомыми величинами задачи?
2) Какой параметр задачи служит критерием эффективности (оптимальности) решения? (это может быть: прибыль, время, количество отходов и т.д.)
3) В каком направлении должно изменяться значение этого параметра (к 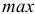 или к
или к 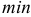 ) для достижения наилучших результатов?
) для достижения наилучших результатов?
4) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
а) Искомые величины являются переменными задачи, которые как правило обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде 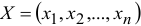 .
.
б) Цель решения записывается в виде целевой функции, обозначаемой, например, 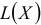 . Математическая формула ЦФ
. Математическая формула ЦФ 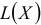 отражает способ расчета значений параметра — критерия эффективности задачи.
отражает способ расчета значений параметра — критерия эффективности задачи.
в) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничении. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия.
В процессе записи математической модели целесообразно указывать единицы измерения переменных задачи, целевой функции и всех ограничений.
| Решение задач по математическому программированию |
Контрольная работа №1
Фабрика производит два вида красок: первый — для наружных, а второй — для внутренних работ. Для производства красок используются два ингредиента: 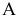 и
и 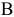 . Известны расходы ингредиентов
. Известны расходы ингредиентов 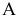 и
и 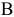 на 1 т соответствующих красок и максимально возможные суточные запасы этих ингредиентов на складе. Данные по расходам ингредиентов на краски первого и второго вида представлены в таблице.
на 1 т соответствующих красок и максимально возможные суточные запасы этих ингредиентов на складе. Данные по расходам ингредиентов на краски первого и второго вида представлены в таблице.

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Решение:
В задаче требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:
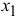 — суточный объем производства краски 1-го вида, [т краски/сутки];
— суточный объем производства краски 1-го вида, [т краски/сутки]; 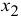 — суточный объем производства краски 2-го вида, [т краски/сутки].
— суточный объем производства краски 2-го вида, [т краски/сутки].
В условии задачи сформулирована цель — добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи красок обоих видов, необходимо знать объемы производства красок, т.е. 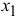 и
и 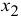 т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов — согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1 -го вида равен З
т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов — согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1 -го вида равен З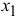 , тыс. руб. в сутки, а от продажи краски 2-го вида — 2
, тыс. руб. в сутки, а от продажи краски 2-го вида — 2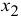 тыс. руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
тыс. руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)

Возможные объемы производства красок 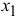 и
и 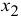 ограничиваются следующими условиями:
ограничиваются следующими условиями:
• количество ингредиентов 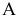 и
и 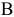 , израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
• согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;
• объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;
• объемы производства красок не могут быть отрицательными.
Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:
1) расходом ингредиентов;
2) рыночным спросом на краску;
3) неотрицательностью объемов производства.
Ограничения по расходу любого из ингредиентов имеют следующую содержательную форму записи:
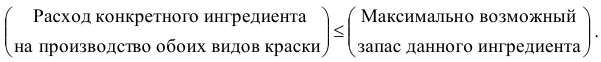
Запишем эти ограничения в математической форме.
Левая часть ограничения — это формула расчета суточного расхода конкретного ингредиента на производство красок. Так из условия известен расход ингредиента 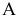 на производство 1 т краски 1-го вида (1 т ингр.
на производство 1 т краски 1-го вида (1 т ингр. 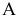 ) и 1 т краски 2-го вида (2 т ингр.
) и 1 т краски 2-го вида (2 т ингр. 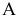 ). Тогда на производство
). Тогда на производство 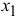 т краски 1-го вида и
т краски 1-го вида и 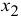 т краски 2-го вида потребуется
т краски 2-го вида потребуется 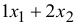 т ингр.
т ингр. 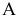 .
.
Правая часть ограничения — это величина суточного запаса ингредиента на складе, например, 6 т ингредиента 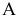 в сутки. Таким образом, ограничение по расходу
в сутки. Таким образом, ограничение по расходу 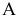 имеет вид
имеет вид
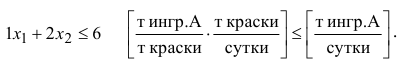
Аналогична математическая запись ограничения по расходу 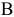
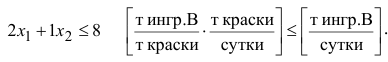
Примечание. Следует всегда проверять размерность левой и правой частей каждого из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибке при составлении ограничений.
Ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го вида имеет
содержательную форму

и математическую форму
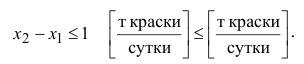
Ограничение по суточному объему производства краски 1-го вида имеет
содержательную форму
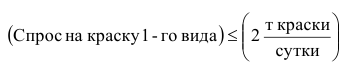
и математическую форму
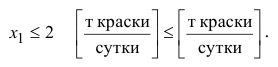
Неотрицательность объемов производства задается как
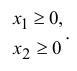
Таким образом, математическая модель этой задачи имеет вид
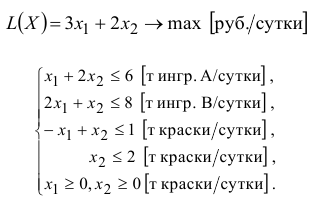
Для задач линейного программирования, содержащих только две переменные 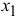 и
и 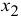 применим графический способ решения. Этот способ основан на том факте, что в случае двух переменных множество допустимых решений можно построить на двухмерной плоскости.
применим графический способ решения. Этот способ основан на том факте, что в случае двух переменных множество допустимых решений можно построить на двухмерной плоскости.
| Примеры решения задач по математическому программированию |
Графический метод решения задач линейного программирования
Графический метод довольно прост и нагляден для решения задач ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи. Каждое из неравенств задачи ЛП определяет на координатной плоскости 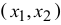 некоторую полуплоскость, а система неравенств в целом — пересечение соответствующих полуплоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки
некоторую полуплоскость, а система неравенств в целом — пересечение соответствующих полуплоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки 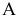 и
и 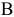 принадлежат этой фигуре, то и весь отрезок
принадлежат этой фигуре, то и весь отрезок 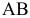 принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.
принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.
Оптимальное решение всегда находится на границе ОДР т.е. ЦФ
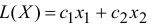
принимает свое 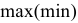 значение на границе области, точнее в ее угловых точках.
значение на границе области, точнее в ее угловых точках.
При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений — единственная точка; задача не имеет решений.
| Заказать работу по математическому программированию |
Методика решения контрольных работ линейного программирования графическим методом
I. В ограничениях задачи замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.
II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи. Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.
Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку 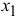 и
и 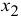 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси 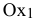 и правее оси
и правее оси 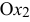 , т.е. в 1-м квадранте. Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.
, т.е. в 1-м квадранте. Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.
III. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решений, о чем сделайте соответствующий вывод.
IV. Если ОДР — не пустое множество, то определите координаты угловых точек. Определение координат сводится к решению системы соответствующих линейных уравнений.
V. Подставьте координаты угловых точек в уравнение для ЦФ и найдите 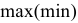 значение целевой функции.
значение целевой функции.
Можно вместо перебора всех угловых точек (пункт IV, ) произвести следующие действия:
IV.a Провести вектор, координатами которого служат коэффициенты в уравнении с целевой функцией. Сдвигать прямую перпендикулярную построенному вектору от начала по направлению вектора до момента, когда пересечение сдвигаемой прямой с ОДР будет составлять одну точку.
V.a Координаты найденной точки будут являться оптимальным планом, а если их подставить в уравнение целевой функции, то получим ее 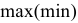 значение.
значение.
| Помощь по математическому программированию |
Контрольная работа №2
Найдем оптимальное решение задачи о красках, математическая модель которой имеет вид:
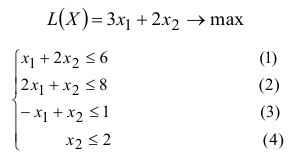
Решение:
Построим прямые ограничений (рис. 1).
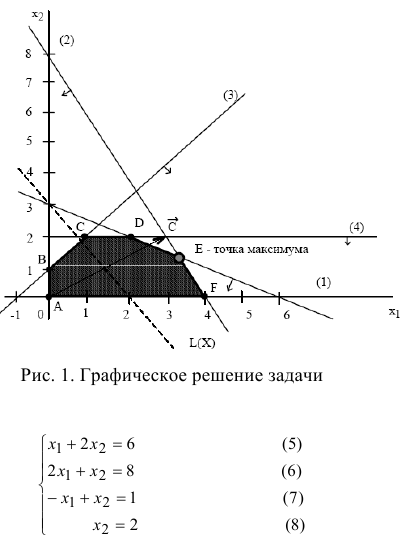
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим 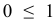 , что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис. 1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник
, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис. 1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник 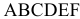 .
.
Найдем координаты точек пересечения прямых ограничений, т.е. координаты угловых точек. В некоторых случаях хороший рисунок позволяет сразу определять координаты угловых точек.
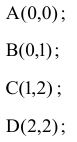
Для определения координаты точки 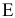 решим систему уравнений с ограничениями (5) и (6).
решим систему уравнений с ограничениями (5) и (6).
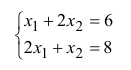
Решая данную систему получаем:
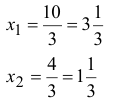
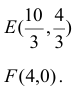
Найдем значение целевой функции в угловых точках, т.е. подставим их координаты в уравнение
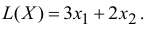
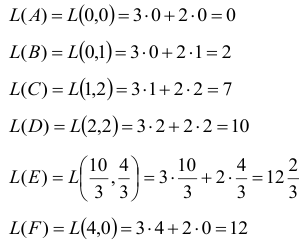
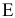 — это точка максимума ЦФ.
— это точка максимума ЦФ.
Таким образом, наилучшим режимом работы фирмы является ежесуточное производство краски 1-го вида в объеме 3 1/3 т и краски 2-го вида в объеме 1 1/3 т. Доход от продажи красок составит 12 2/3 тыс. руб. в сутки.
Решая графическим методом, предполагающим построение целевого вектора, проводим вектор, координатами которого служат коэффициенты в уравнении с целевой функцией {3,2}; сдвигая прямую, перпендикулярную построенному вектору (от начала к концу), найдем точку, являющуюся последней в пересечении сдвигаемой прямой с ОДР (это точка 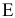 ), ее координаты, найденные из решения системы соответствующих уравнений, будут являться оптимальным планом, а значение целевой функции в ней будет max.
), ее координаты, найденные из решения системы соответствующих уравнений, будут являться оптимальным планом, а значение целевой функции в ней будет max.
В более общем случае разработан и широко применяется универсальный метод решения любой задачи ЛП, называемый симплекс-методом.
Симплекс — метод, как метод решения задач ЛП был предложен американским математиком-экономистом Данцигом в 1951 году.
Графически симплекс метод представляет из себя передвижение по выпуклому многограннику от вершины к вершине, при этом значение целевой функции на каждом шаге улучшается до тех пор, пока не достигается оптимум.
Идея симплекс — метода состоит в том, чтобы преобразовать уравнение содержащее целевую функцию к виду:
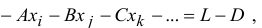
т.к. в этом случае становиться возможным выразить
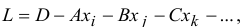
а в силу того что перед нами ставится задача максимизировать 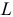 , то эта задача достигается в случае, когда все переменные, присутствующие в данном уравнении, принимают нулевые значения (т.к. переменные не отрицательны по условию).
, то эта задача достигается в случае, когда все переменные, присутствующие в данном уравнении, принимают нулевые значения (т.к. переменные не отрицательны по условию).
| Задачи математического программирования |
Симплекс метод решения задач линейного программирования
Алгоритм решения задачи при помощи симплекс метода:
- Вводятся переменные, позволяющие систему неравенств превратить в систему уравнений. (Ограничение-неравенство исходной задачи ЛП, имеющее вид
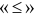 , можно преобразовать в ограничение-равенство добавлением к его левой части некоторой новой неотрицательной переменной, а ограничение-неравенство вида
, можно преобразовать в ограничение-равенство добавлением к его левой части некоторой новой неотрицательной переменной, а ограничение-неравенство вида 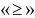 в ограничение равенство вычитанием из его левой части неотрицательной переменной. Переменные, вводимые для преобразования ограничений-неравенств в ограничения -равенства называют дополнительными. Их число равно числу преобразуемых неравенств.)
в ограничение равенство вычитанием из его левой части неотрицательной переменной. Переменные, вводимые для преобразования ограничений-неравенств в ограничения -равенства называют дополнительными. Их число равно числу преобразуемых неравенств.) - Выбирается переменная (рабочая переменная) входящая в целевую функцию с
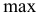 коэффициентом (Уничтожать переменные целесообразно, начиная с самой «неподходящей для итогового вида», таким образом, выбирается переменная, входящая в уравнение с целевой функцией, которую уничтожим в первую очередь).
коэффициентом (Уничтожать переменные целесообразно, начиная с самой «неподходящей для итогового вида», таким образом, выбирается переменная, входящая в уравнение с целевой функцией, которую уничтожим в первую очередь). - Сравниваются частные от деления свободных членов на коэффициенты при этой переменной и выбирается строка с
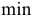 > 0 частным от деления (рабочее уравнение). (Выбирается уравнение, в котором рабочая переменная имеет «наибольший вес» относительно других переменных).
> 0 частным от деления (рабочее уравнение). (Выбирается уравнение, в котором рабочая переменная имеет «наибольший вес» относительно других переменных). - Рабочее уравнение нормируется (т.е. делится на коэффициент перед рабочей переменной), из остальных строк исключаем рабочую переменную методом Гаусса. (Проведение данной операции обусловлено необходимостью исключить возможность проявления уже исключенной из уравнения с целевой функцией переменной в дальнейшем при последующих преобразованиях.)
- Проверяется, существуют ли положительные коэффициенты перед переменными в уравнении с целевой функцией: если да, то возвращаются к пункту 2, если нет, то решение закончено.
Контрольная работа №3
В качестве примера рассмотрим контрольную решенную графическим методом, задачу про краски.
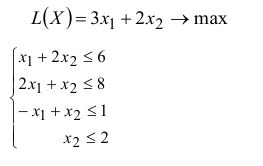
Решение:
Введем свободные переменные 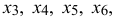 для того, чтобы систему неравенств превратить в систему уравнений.
для того, чтобы систему неравенств превратить в систему уравнений.
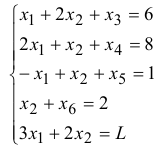
Выбираем переменную, входящую в целевую функцию с максимальным коэффициентом, это 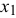 . Сравниваем частные от деления свободных членов на коэффициенты при
. Сравниваем частные от деления свободных членов на коэффициенты при 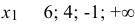 . Выбираем строку с
. Выбираем строку с 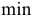 > 0 частным от деления и нормируем ее, из остальных строк исключаем
> 0 частным от деления и нормируем ее, из остальных строк исключаем 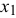 методом Гаусса.
методом Гаусса.
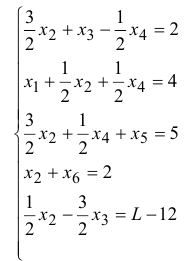
Выбираем переменную, входящую в целевую функцию с 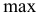 коэффициентом, это
коэффициентом, это 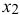 . Сравниваем частные от деления свободных членов на коэффициенты при
. Сравниваем частные от деления свободных членов на коэффициенты при 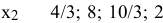 . Выбираем строку с
. Выбираем строку с 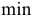 > 0 частным от деления и нормируем ее, из остальных строк исключаем
> 0 частным от деления и нормируем ее, из остальных строк исключаем 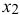 методом Гаусса.
методом Гаусса.
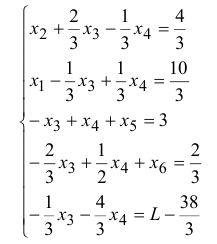
Так как все коэффициенты перед переменными в уравнении с целевой функцией < 0, то решение законченно.
В силу не отрицательности переменных из уравнения, содержащего целевую функцию следует, что она достигает максимального значения, в случае, когда
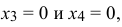
в этом случае
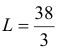
| Задача линейного программирования |
Анализ чувствительности оптимального решения одноиндексных задач линейного программирования
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением — недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
Анализ сокращения или увеличения ресурсов:
• на сколько можно увеличить (ограничения типа 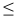 ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
• на сколько можно уменьшить (ограничения типа 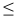 ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
- Увеличение (ограничения типа
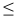 ) запаса какого из ресурсов наиболее выгодно?
) запаса какого из ресурсов наиболее выгодно? - Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?
Методика графического анализа чувствительности оптимального решения:
1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничении)
Проанализируем чувствительность оптимального решения задачи о производстве красок. ОДР задачи (рис. 1) — многоугольник 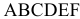 . В оптимальной точке
. В оптимальной точке 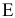 пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты
пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты 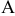 и
и 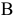 ) — дефицитными. Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ
) — дефицитными. Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ 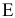 соответствует суточному производству 3 1/3 т краски 1-го вида и 1 1/3 т краски 2- го вида. В производстве красок используются ингредиенты
соответствует суточному производству 3 1/3 т краски 1-го вида и 1 1/3 т краски 2- го вида. В производстве красок используются ингредиенты 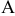 и
и 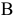 . Суточный запас на складе ингредиентов
. Суточный запас на складе ингредиентов 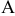 и
и 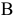 — это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке
— это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке 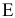 расходуется:
расходуется:
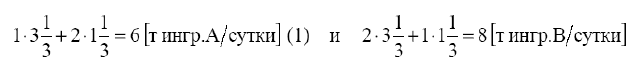
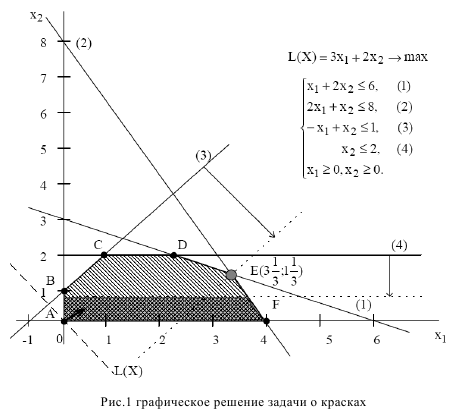
Таким образом, понятие «связывающие ограничения» (1) и (2) означает, запасы ингредиентов 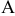 и
и 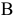 что при производстве красок в точке
что при производстве красок в точке
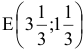
расходуются полностью и по этой причине невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если фирма сможет увеличить суточные запасы ингредиентов, то это позволит увеличить выпуск красок. В связи с этим возникает вопрос: до какого уровня целесообразно увеличить запасы ингредиентов и на сколько при этом увеличится оптимальное производство красок?
Правило № 1
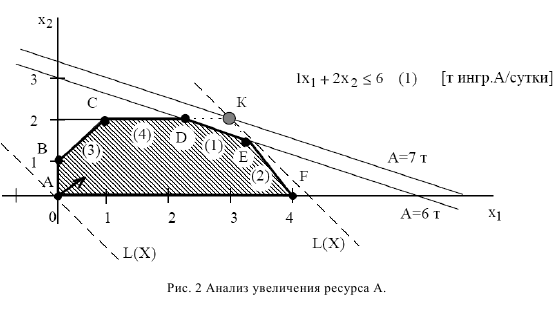
Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения, необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным. При прохождении прямой (1) через точку 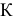 (рис. 2) многоугольник
(рис. 2) многоугольник 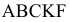 становится ОДР, а ограничение (1) — избыточным. Действительно, если удалить прямую (1), проходящую через точку
становится ОДР, а ограничение (1) — избыточным. Действительно, если удалить прямую (1), проходящую через точку 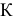 , то ОДР
, то ОДР 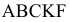 не изменится. Точка
не изменится. Точка 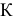 становится оптимальной, в этой точке ограничения (2) и (4) становятся связывающими.
становится оптимальной, в этой точке ограничения (2) и (4) становятся связывающими.
Правило № 2
Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения, необходимо:
1) определить координаты точки 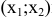 , в которой соответствующее ограничение становится избыточным;
, в которой соответствующее ограничение становится избыточным;
2) подставить координаты 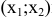 в левую часть соответствующего ограничения.
в левую часть соответствующего ограничения.
Координаты точки 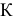 (3;2) находятся путем решения системы уравнений прямых (2) и (4). Т.е. в этой точке фирма будет производить 3 т краски 1-го вида и 2 т краски 2-го вида. Подставим
(3;2) находятся путем решения системы уравнений прямых (2) и (4). Т.е. в этой точке фирма будет производить 3 т краски 1-го вида и 2 т краски 2-го вида. Подставим
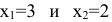
в левую часть ограничения (1) и получим максимально допустимый запас ингредиента 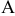 .
.
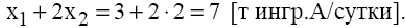
Дальнейшее увеличение запаса ингредиента 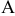 нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис. 2). Доход от продажи красок в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты (3;2) в выражение ЦФ
нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис. 2). Доход от продажи красок в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты (3;2) в выражение ЦФ
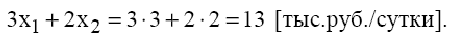
Рассмотрим вопрос о целесообразности увеличения запаса ингредиента 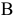 . Согласно правилу № 1, соответствующее ограничение (2) становится избыточным в точке
. Согласно правилу № 1, соответствующее ограничение (2) становится избыточным в точке 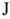 , в которой пересекаются прямая (1) и ось переменной
, в которой пересекаются прямая (1) и ось переменной 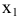 (рис. 3). Многоугольник
(рис. 3). Многоугольник 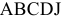 становится ОДР, а точка
становится ОДР, а точка 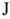 (6;0) -оптимальным решением.
(6;0) -оптимальным решением.
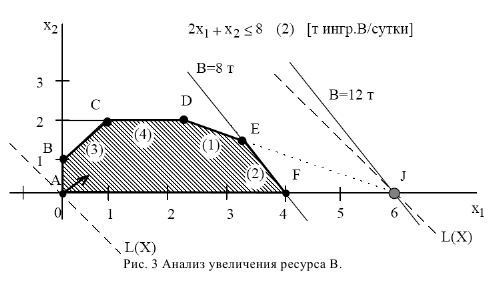
В точке 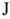 выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит:
выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит:
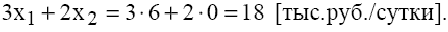
Чтобы обеспечить такой режим работы, согласно правилу № 2, запас ингредиента 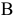 надо увеличить до величины:
надо увеличить до величины:
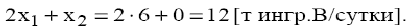
Ограничения (3) и (4) являются не связывающими, т.к. не проходят через оптимальную точку 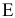 (см. рис. 1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке
(см. рис. 1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке 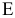 .
.
Например, увеличение (уменьшение) спроса на краску 2-го вида будет соответствовать перемещению прямой ограничения 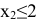 (4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку
(4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку 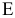 максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой
максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой 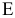 (см. правило № 3.3). Из рис. 1 видно, что дальнейшее перемещение (4) приведет к тому, что точка
(см. правило № 3.3). Из рис. 1 видно, что дальнейшее перемещение (4) приведет к тому, что точка 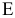 будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки
будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки 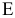 .
.
Правило № 3
Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение, необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой.
Правило № 4
Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение, необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.
Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке
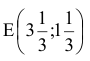
используем правило № 4.
Подставляем в левую часть ограничения (4) координаты точки 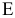 , получаем
, получаем
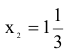
Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность полученного ранее решения, равен 1 1/3 т краски в сутки. Экономический смысл ограничения (3)
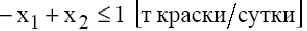
в том, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки 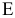 . Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка
. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка 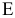 остается оптимальной, является пересечение с точкой
остается оптимальной, является пересечение с точкой 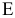 (см. рис. 3.1). Согласно правилу № 4, подставим координаты точки
(см. рис. 3.1). Согласно правилу № 4, подставим координаты точки 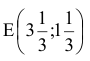 в левую часть ограничения (3)
в левую часть ограничения (3)
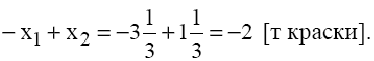
Получаем, что разность спросов на краску 2-го и 1-го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку 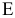 означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1 -го вида
означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1 -го вида
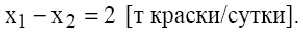
Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке 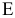 не изменится, составляет 2 т краски в сутки. Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.
не изменится, составляет 2 т краски в сутки. Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.
Результаты анализа ресурсов задачи
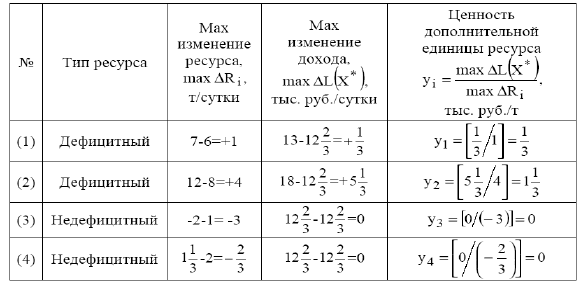
Вторая задача анализа на чувствительность
Анализ представленной таблицы показывает, что к улучшению оптимального решения, т.е. к увеличению суточного дохода приводит увеличение дефицитных ресурсов. Для определения выгодности увеличения этих ресурсов используют понятие ценности дополнительной единицы 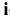 -го ресурса
-го ресурса 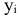
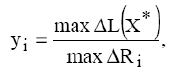
где 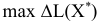 — максимальное приращение оптимального значения ЦФ;
— максимальное приращение оптимального значения ЦФ; 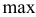
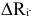 — максимально допустимый прирост объема
— максимально допустимый прирост объема 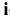 -го ресурса.
-го ресурса.
Например, из табл. следует, что увеличение суточного запаса ингредиента 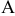 [ограничение (1)] на 1 т позволит получить дополнительный доход, равный
[ограничение (1)] на 1 т позволит получить дополнительный доход, равный 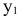 =1/3тыс.руб./сутки, в то время как увеличение запаса
=1/3тыс.руб./сутки, в то время как увеличение запаса 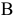 [ограничение (2)] на 1 т принесет
[ограничение (2)] на 1 т принесет 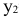 =1 1/3 тыс.руб./сутки. Недефицитные ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.
=1 1/3 тыс.руб./сутки. Недефицитные ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.
Вывод: дополнительные вложения в первую очередь необходимо направлять на увеличение ресурса 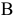 , а лишь потом на ресурс
, а лишь потом на ресурс 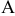 . Изменять недефицитные ресурсы нет необходимости.
. Изменять недефицитные ресурсы нет необходимости.
Третья задача анализа на чувствительность
Графический анализ допустимого диапазона изменении цен Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой вокруг оптимальной точки. Так, при увеличении коэффициента ЦФ 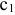 или уменьшении
или уменьшении 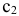 целевая прямая вращается по часовой стрелке. При уменьшении
целевая прямая вращается по часовой стрелке. При уменьшении 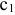 или же увеличении
или же увеличении 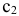 целевая прямая вращается против часовой стрелки (рис. 4). При таких поворотах точка
целевая прямая вращается против часовой стрелки (рис. 4). При таких поворотах точка 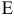 будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка
будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка 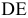 .
.
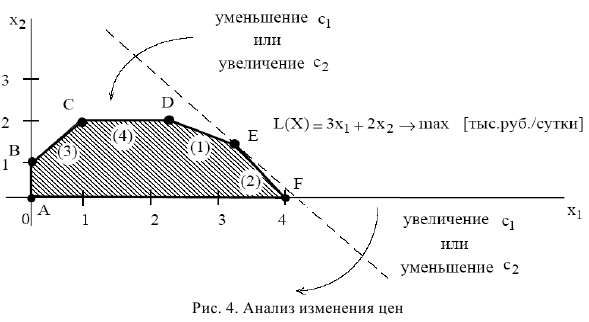
При совпадении с прямой (2) оптимальным решением будут точки отрезка 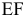 . Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно
. Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно 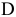 или
или 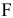 .
.
Допустим, что цена на краску 2-го вида не меняется, т.е. зафиксируем значение целевого коэффициента 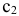 . Проанализируем графически результаты изменения значения целевого коэффициент
. Проанализируем графически результаты изменения значения целевого коэффициент 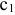 , т.е. цены на краску 1-го вида. Оптимальное решение в точке
, т.е. цены на краску 1-го вида. Оптимальное решение в точке 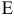 не будет меняться при увеличении
не будет меняться при увеличении 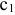 до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке
до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке 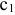 не будет меняться при уменьшении
не будет меняться при уменьшении 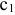 до тех пор, пока целевая прямая не совпадет с прямой (1).
до тех пор, пока целевая прямая не совпадет с прямой (1).
Аналитический поиск допустимого диапазона изменения цен Совпадение в процессе вращения целевой прямой с прямой ограничения означает, что углы их наклона относительно горизонтальной оси сравнялись, а значит, стали равны тангенсы углов наклона этих прямых.
Правило 5
Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например 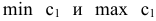 , необходимо приравнять тангенс угла наклона целевой прямой ЦФ
, необходимо приравнять тангенс угла наклона целевой прямой ЦФ 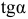 поочередно к тангенсам углов наклона прямых связывающих ограничений, например
поочередно к тангенсам углов наклона прямых связывающих ограничений, например 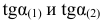 (рис. 5 и 6)
(рис. 5 и 6)
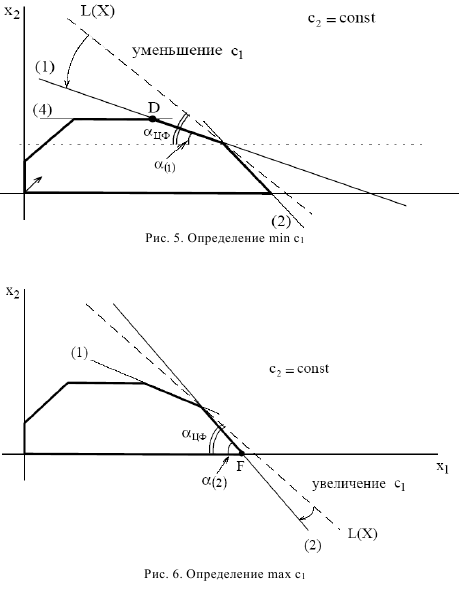
Определим насколько максимально может снизиться цена на краску 1 -го вида, не изменяя оптимальную точку 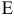 . Для этого применим правило № 5 и формулу расчета тангенса угла наклона прямой (рис. 7).
. Для этого применим правило № 5 и формулу расчета тангенса угла наклона прямой (рис. 7).
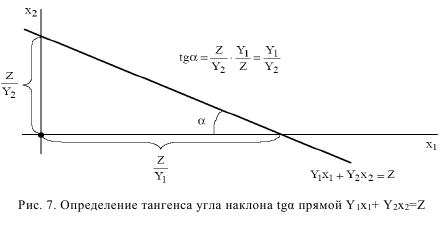
Определим тангенсы углов наклона:
1) целевой прямой
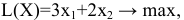
учитывая, что 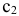 =2 фиксировано
=2 фиксировано
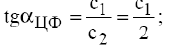
2) связывающего ограничения
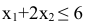
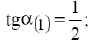
3) связывающего ограничения
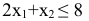
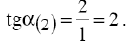
Для нахождения 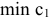 целевая прямая должна совпасть с прямой (1) (рис. 5):
целевая прямая должна совпасть с прямой (1) (рис. 5):
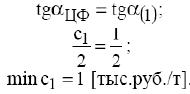
Для нахождения 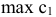 целевая прямая должна совпасть с прямой (2) (рис. 6):
целевая прямая должна совпасть с прямой (2) (рис. 6):
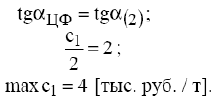
Возможно эти страницы вам будут полезны:

