Перед математикой встала задача: расширить поле действительных чисел путем присоединения к нему новых чисел так, чтобы расширенное множество образовывало числовое поле, в котором было бы выполнимо действие извлечения корней. Следовательно, расширенное поле должно содержать все действительные числа и в нем должно быть разрешимо уравнение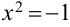 
( т. е. выполнимо извлечение корней — обратное действие возведению в степень).
Число, квадрат которого равен — 1, принято обозначать буквой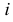 
и называть мнимой единицей: 
.
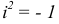Новое поле должно содержать все числа вида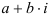 
, где 
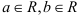, а 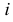— мнимая единица. Эти числа называются комплексными числами.
Число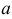 
принято называть действительной частью, а выражение 
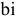— мнимой частью комплексного числа. Число 
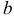называется коэффициентом при мнимой части.
Два комплексных числа считаются равными, если равны их действительные части и коэффициенты при мнимых частях.
Другими словами,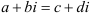 
тогда и только тогда, когда 
.
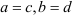Для комплексных чисел соотношения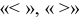 
не имеют смысла.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Задачи, приводящие к дифференциальным уравнениям с примером решения |
| Числовые поля |
| Действия с комплексными числами в алгебраической форме |
| Решение алгебраических уравнений в поле комплексных чисел |
