Оглавление:
Классификация точек разрыва функции
Пусть функция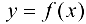 
определена в некоторой проколотой окрестности точки 
.
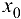Определение 4.6. Точка 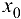называется точкой разрыва функции 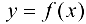, если функция в этой точке не определена или же не является в ней непрерывной.
Определение 4.7. Точка 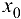называется точкой устранимого разрыва функции 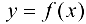(рис. 4.1), если
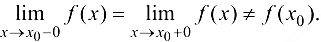
Чтобы устранить разрыв в точке 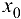, достаточно принять 
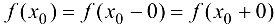. В этом случае говорят, что функция доопределена по непрерывности в точке .
Определение 4.8. Точка 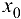называется точкой разрыва первого рода функции 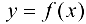(рис. 4.2), если в этой точке существуют конечные односторонние пределы, но они не равны между собой, т. е.
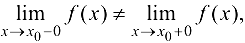
где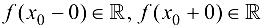 
.
Разность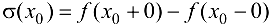 
представляет скачок функции 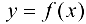в точке .
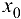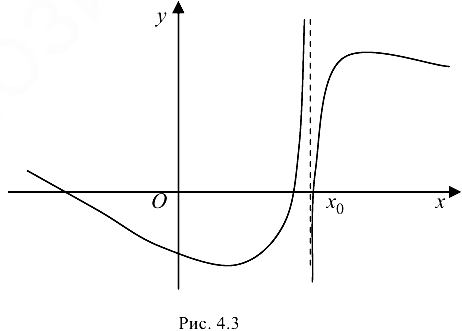
Определение 4.9. Точка 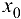называется точкой разрыва второго рода функции 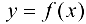(рис. 4.3), если в этой точке хотя бы один из односторонних пределов равен 
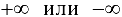, или вообще не существует. Причем если хотя бы один предел не существует, то точка 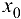называется точкой неопределенности, если хотя бы один из односторонних пределов равен 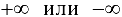, то точка 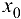называется точкой бесконечного скачка.
Пример 4.2.
Определить точки разрыва функции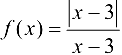 
и их характер. Построить схематичный график функции.
Решение:
Функция 
определена и непрерывна на всей числовой прямой, за исключением точки 
, т. е.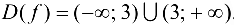 
. Следовательно, точка 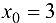является точкой разрыва дайной функции. Выясним характер точки разрыва, для чего найдем односторонние пределы в этой точке. Так как
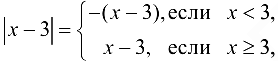
то
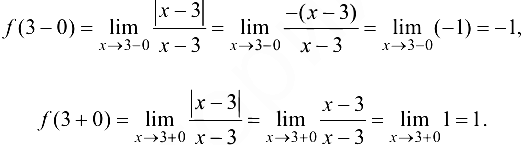
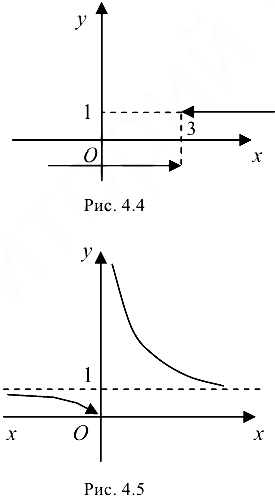
Так как односторонние пределы конечны, по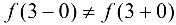 
, то в точке 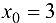функция имеет разрыв первого рода.
Скачок функции составляет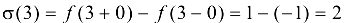 
.
График функции представлен па рис. 4.4.
Ответ.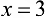 
— точка разрыва первого рода.
Пример 4.3.
Определить точки разрыва функции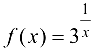 
и их характер. Построить схематичный график функции.
Решение:
Функция 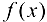определена и непрерывна на всей числовой прямой, за исключением точки 
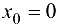, т. е. 
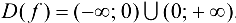. Следовательно, точка 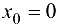является точкой разрыва данной функции. Выясним характер точки разрыва, для чего найдем односторонние пределы в этой точке
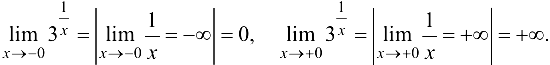
Следовательно, в точке 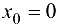данная функция имеет точку разрыва второго рода, а именно бесконечный скачок. Для схематичного построения графика найдем 
.
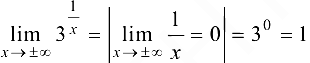График функции представлен па рис. 4.5.
Ответ: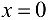 
— точка разрыва второго рода.
Пример 4.4.
Дана функция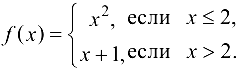 
Является ли она непрерывной? Если нет, определить точки ее разрыва и их характер. Построить схематичный график функции.
Решение:
Данная функция непрерывна для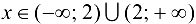 
, так как на каждом из этих интервалов формулы, задающие функцию, определяют элементарные непрерывные функции. Точкой разрыва может быть лишь точка 
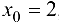, в которой меняется аналитическое выражение функции 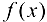. Найдем односторонние пределы:
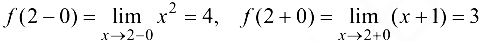
Так как односторонние пределы конечны, но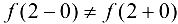 
, то в точке 
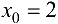функция имеет разрыв первого рода. Скачок функции составляет 
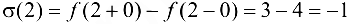. График функции представлен па рис. 4.6.
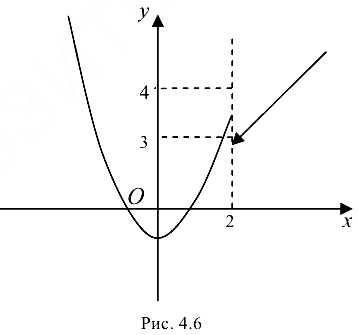
Ответ.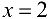 
— точка разрыва первого рода.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
