Касательные плоскости и нормаль к поверхности
Плоскостью, касательной к поверхности в некоторой ее точке, называют плоскость, в которой можно провести две прямые линии, пересекающиеся в точке касания, касательные к двум пересекающимся в этой же точке линиям, принадлежащим поверхности.
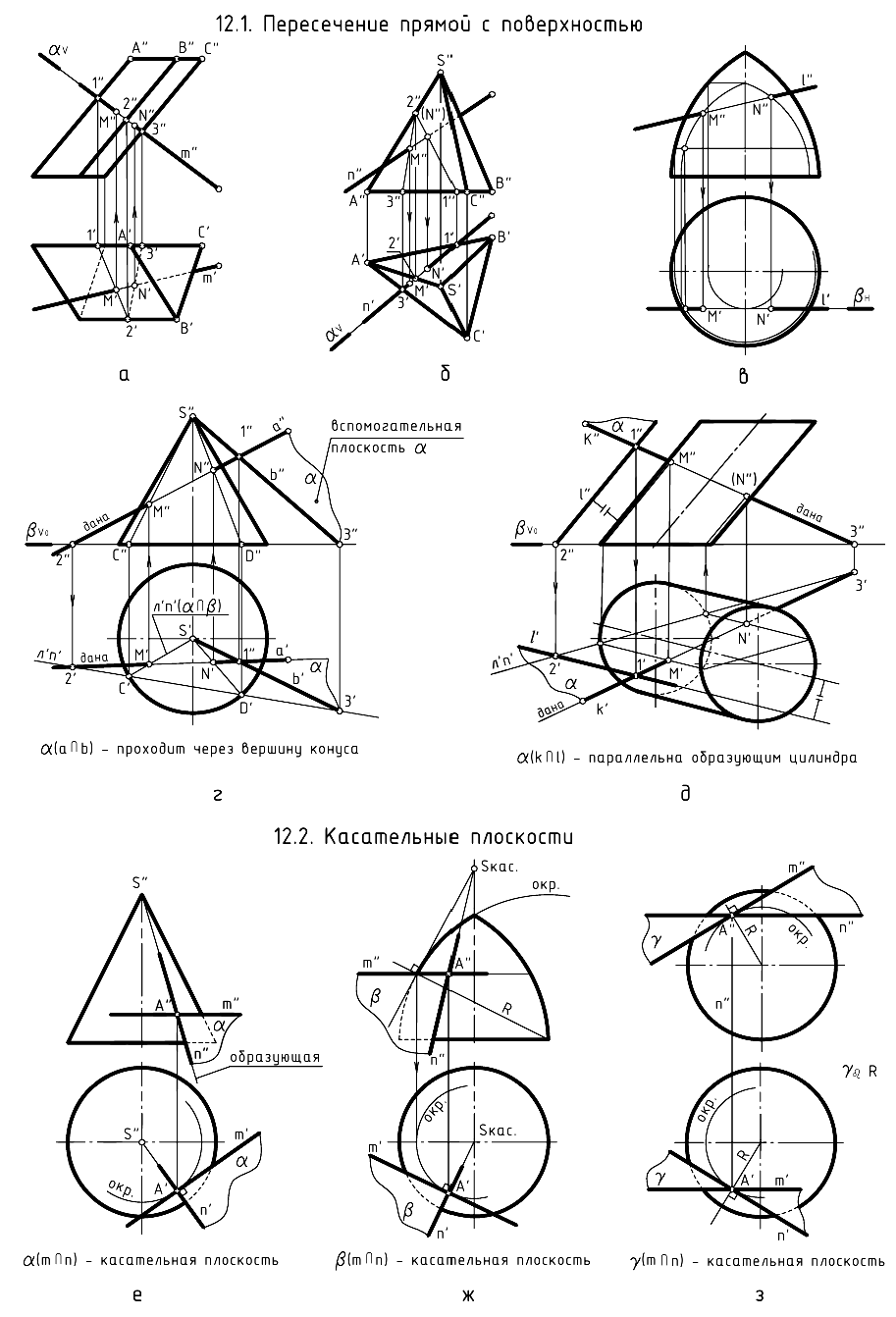
На чертеже касательную плоскость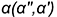 
однозначно можно задать проекциями двух пересекающихся прямых 
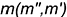и 
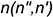. Эти линии строят касательно к проекциям двух пересекающихся в точке касания линий, принадлежащих поверхности. На рис. 12.4 линия 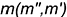является касательной к линии окружности 
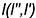, проходящей через точку касания 
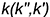по поверхности цилиндра, а пересекающаяся с ней в этой точке линия 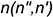сливается с линией 
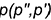— образующей цилиндра.
Аналогичные действия (рис. 12.8, е, ж, з) выполнены и при построении касательных плоскостей к поверхностям прямого кругового конуса, самопересекающегося тора и сферы, касающихся этих поверхностей в некоторой точке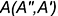 
. Пересекающиеся прямые 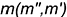и 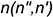, задающие касательные плоскости 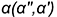к ним, являются касательными к окружностям, построенным на этих поверхностях вращения и пересекающимся в точке касания 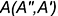. Следует отметить одну особенность при построении прямой , касательной к линии меридионального сечения поверхности самопересекающегося тора (рис. 12.8, ж).
Для упрощения построений вначале строят касательную к этой линии, параллельной фронтальной плоскости проекций, определяют на оси вращения тора точку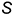 
, через которую проходят касательные ко всем точкам, расположенным на той же параллели поверхности, что и заданная точка касания 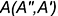а затем строят необходимую касательную .
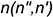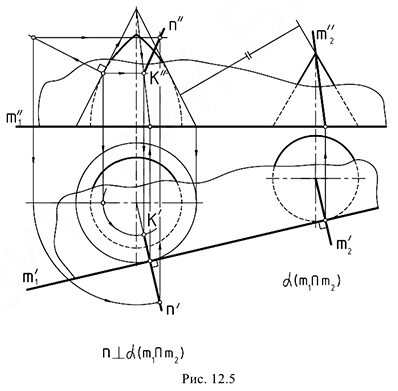
Эти построения использовались также для определения точки касания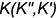 
на поверхности самопересекающегося тора в задаче на рис. 12.5, где необходимо было задать общую касательную плоскость к поверхностям самопересекающегося тора и прямого кругового конуса. Ключом к решению задачи явилось заключение самопересекающегося тора в коническую поверхность с тем же углом наклона образующих, что и у заданного конуса (справа).
Общая касательная плоскость задана пересекающимися прямыми, из которых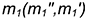 
, являющаяся горизонтальным следом плоскости, построена, как касательная к следам указанных конических поверхностей, а прямая 
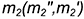сливается с одной из образующих заданного конуса. Эта образующая является и геометрическим элементом касания построенной плоскости 
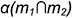с поверхностью заданного конуса. Поверхности самопересекающегося тора эта плоскость касается в точке 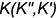которая найдена благодаря выше рассмотренным построениям и образующей второго конуса, охватывающего тор.
На рассматриваемом чертеже показано также построение нормали 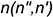, к поверхности самопересекающегося тора в точке 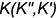. Условием для построения нормали является ее перпендикулярность к плоскости, касательной к поверхности в той же точке. Вначале нормаль построена к очерковой образующей тора, затем на ней взята произвольная точка и выполнен ее поворот вокруг оси тора в положение, в котором она окажется расположенной в плоскости, перпендикулярной построенной касательной плоскости (направления указанных перемещений показаны стрелками).
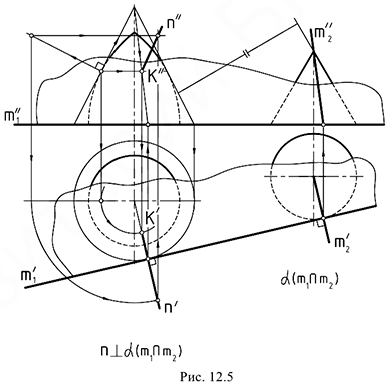
На рис. 12.6 показано построение точек пересечения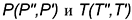 
фронтальной прямой 
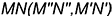с поверхностью 1/4 кольцевого тора и построение касательной плоскости к этой поверхности в одной из построенных точек, например, 
.
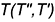Точк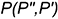и 
и 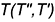найдены благодаря заключению заданной прямой 
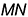во фронтальную плоскость 
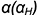и построению проекций линии пересечения по точкам 
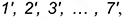, крайние из которых 
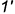и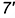 
взяты в местах пересечения горизонтального очерка плоскостью тора, а остальные — произвольно на горизонтальном следе ан секущей плоскости. Для дальнейших построений использовались горизонтальные сечения поверхности тора плоскостями.
Для задания касательной плоскости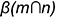 
одна из задающих ее пересекающихся прямых 
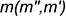построена как касательная к линии кольцевого сечения поверхности тора в точке 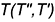, а вторая — как касательная прямая 
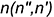к линии окружности осевого сечения поверхности тора. Для более точного построения второй прямой была найдена проекция 
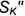точки на оси вращения тора, в которой сходятся все касательные прямые к поверхности тора во всех точках, находящихся на той же параллели, что и точка .
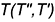Структуризация материала двенадцатой лекции в рассмотренном объеме схематически представлена на рис. 12.7 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 12.8).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
