Оглавление:





Касательная к. плоской кривой
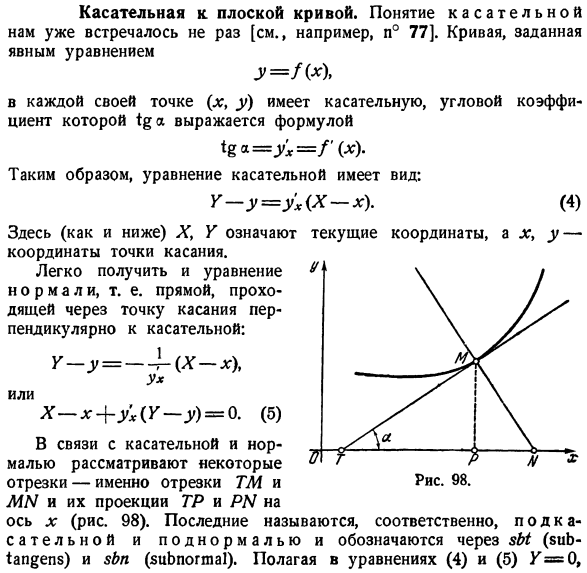
Касательная к. плоской кривой. Мы уже много раз сталкивались с понятием касательности[например, см. n°77].Кривая, заданная явным уравнением У = РХ \ Каждая точка ( * , y) имеет касательную, угловой коэффициент которой выражается формулой: Итак, форма касательного уравнения выглядит следующим образом: Г-г = Ух {х-х (4) Здесь (как показано ниже) X> Y означает текущие координаты, а x, y-координаты контактов. Легко получить прямую через нормальное уравнение, то есть точку касательной, перпендикулярную касательной: Вау. Ыы = р (х-х)、 Или ХХ + ух(г)= Б(5) В связи с касательной и нормалью учитываются некоторые отрезки-а именно отрезки TM и WE и их проекции TP и PY ось Х (рис. 98).Последний называется по касательным и ненормальным соответственно$ S ($b * * apgepz) и sbn (zbpogsh!). обозначается через a).
Предполагая, что это уравнение вблизи интересующей точки эквивалентно уравнению в виде (1)), кривая в этой точке, очевидно, имеет касательную линию (4). Людмила Фирмаль
- Принимая уравнения(4)и (5)/ = 0、 Это легко вычислить (6) З. Ы. = ТП = м §БН = РУ = ый’х * Ух… * &С= Y_ Вау. Ох * 2ах икс Два 1) например, если парабола y = ax : Уже известные результаты[ссылка сноска 143 стр.]. Затем мы переходим к случаю, когда мы неявно определяем кривую по уравнению (2). n°141, 4), я не могу непосредственно знать производную y»неявной» функции, но я научился выражать ее с помощью известных производных Px и py. Р Х(Х, Y) У-ГУ(.Вт’ ) П’у 0. 0.При предположении, что. Заметим, кстати, что это условие, при котором выражение (2) вблизи рассматриваемой точки кривой оказывается эквивалентным выражению (1) выражения.
Если вы преобразуете его в] касательное уравнение, вы получаете уравнение после простого преобразования. П Х(Х, г) ( -)+ ру(х, г) (гг)=0.(7 )) учитывая совершенную симметрию для x и y, предполагая PxΦ0, ясно, что замена x и y на Rolls дает то же уравнение для tangent. It становится тождеством и перестает быть уравнением частного line. In в этом случае точка (x, y) называется сингулярностью curve. At определенная точка, кривая может на самом деле не иметь определенного касательного! Пример 2) парабола: у =2рлг (рис. 99). мы различаем это уравнение, предполагая, что y является функцией x. Uh-r. So [Ссылка (6)], ненормальность параболы является константой. Это означает простой способ составить нормали, а также тангенс параболы.
- Термин параболическое уравнение, основанный на полученных уравнениях, просто выясните сразу: 2x, или$ M = 2x. Вау. 3) эллипс:^ \ ^ = (рисунок 100). Уравнение (7)дает уравнение касания. ?(Х-х)+ $(г-г)= 0 Учитывая само эллиптическое уравнение, последнее уравнение можно переписать в более простую форму. а * б * Где k = 0, X =-найдено. И так оно и есть.、 Пересечение касательной и оси x T не зависит от y или b. At точки, имеющие абсциссу x, все касательные к различным эллипсам, соответствующие различным значениям b, проходят через одну и ту же точку T на оси X. в случае b-a мы получаем окружность, в которой касательная просто составлена, поэтому точка T сразу определяется, что позволяет нам легко составить касательную эллипса.
Это видно из рисунков. 3 (*8-Ай) и 3 (у * ай) 4) для декартовой: x * + y * 3a * y = 0 обе частные производные в левой части уравнения Исчезает в то же время на origin. As видно из фиг. 95, в сингулярности этой кривой фактически нет определенного касательного. Наконец, рассмотрим кривую, приведенную в параметрическом уравнении(3). в выбранной точке производная x \ = p ’(Если 0 ненулевое, например, больше нуля, то функция* = p sup class=»reg»>®/sup> будет монотонно возрастать[n 111°], затем возрастающая функция b: b-b (x) [n°71], производная функция[n°80].Если вы замените эту функцию на aвместо b、 икс( При преобразовании в уравнение wu =φР) мы видим, что в определенном участке кривой y является функцией π. г = Б(B(х))= F(х)、 Есть и производные.
Таким образом, мы видим, что отрезки кривой, прилегающие к взятой точке, также могут быть представлены явными уравнениями. Людмила Фирмаль
- In в этом случае кривая в этой точке имеет касательную. Угловой коэффициент касательной может быть выражен как и_ Ага. (8) И Подставляя это выражение в тангенс выражения (4), можно легко преобразовать его в форму отношения. (9 )) Х-Х__У-г х * й! * Однако во многих случаях оба знаменателя умножаются на L, и записывается уравнение касательной. (10 )) Х-x_U — ых гг * Если предположить, что производная^ =φ ’sup class=»reg»>®/sup> в выбранной точке ненулевая, то замена*на роль приведет к тому же касательному уравнению. Наш аргумент не может быть применен только в том случае, если обе производные x \и y \исчезают в данной точке одновременно. Такая точка также называется сингулярностью кривой: она может быть не касательной. 5) в качестве примера.
Смотрите также:
Решение задач по математическому анализу
| Механическая работа. | Положительное направление касательной. |
| Аналитическое представление кривых на плоскости. | Случай пространственной кривой. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

