Инвариантность формы (первого) дифференциала

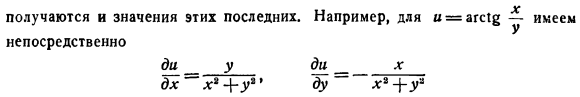
Инвариантность формы (первого) дифференциала

Инвариантность формы (первого) дифференциала. Предположим, что в функции u = f (x, y, r) существуют непрерывные частные производные u * K, u, а x, y, r-функции новых переменных I и Y. * =?(Р«), y = к . «). г = х ((.г „）、 Существуют также непрерывные частные производные (x), x’Y, Y\, r и r*. [N°140] (3） если x, y, r-независимые переменные, то, как известно, вся производная функции равна: Ли = uhx-\ 1У уй + уй Однако, в этом случае, через х, г, р, зависит от переменных I и Y. таким образом, в отношении этих переменных, разница описывается следующим образом: Ли-Энн].И “ Лу. Но и по(3)тоже、 И,= иях-х’,-ыыыы,+ у’g•г’,= У Х•Х * + уй-ю»+ ч’g.

Не только существуют производные комплексных функций относительно t и u, но эти производные также непрерывны относительно t и u. Людмила Фирмаль

• Если вы назначаете эти значения в выражении ли, вы получаете: Ли =(них•х / + гг-г \ +им-р}) у +(них•г + гг-г * + а •г) Лу. Перегруппируйте членов следующим образом: Ложь=их•(Х (Л + Х ’Б * Лу) -уй»[yiL1-\ У1) * Лу)+ + ia * (r ’(*Λ1 | r\, * Λ). Поскольку легко видеть, что выражения в круглых скобках являются только производными функций x, y и r (от I и-y), вы можете написать: Ли =их * ЛК-| 11й•Лу и Иж * ЛГ. теперь он находится в той же дифференциальной форме, что и I, Если x, y, r являются независимыми переменными (но значения символов Lx, Lu и Lr здесь, конечно, разные). Так, для функций некоторых переменных существует инвариантность в виде (первой) производной, а для функций 1 переменной, как и*). x, y и r могут зависеть от различных переменных.

• Например、 * =?(). г-xLuu^®）В этом случае, в любое время х = б (>»О» Г = С*>») * * = Х | (*> В, И.）、 Все предыдущие соображения относятся к этому случаю. Результаты. если x и y являются функциями 1 переменной, то существует следующее выражение: 1 (СХ)= с * Т, Г (Х±Y)= 1х±(1г, д(ху)= м * т + х * юшь;(х \ _y-ых-х-гг л \ 1) -? • Эти выражения также верны, если x и y являются функциями любого числа переменных. * = п(.В.,..), В-в,…это не так. Например, докажем последнюю формулу. Для этого сначала возьмем x и y в качестве независимых переменных. И затем.

В этом предположении мы можем видеть, что производная имеет тот же вид, что и функция переменной t. Людмила Фирмаль

• Основываясь на инвариантности дифференциальных форм, мы можем утверждать, что это выражение также справедливо, если x и y являются функциями любого числа переменных. Доказанные свойства полного дифференцирования и их следствия позволяют упростить расчет дифференциалов. Например че ags18 Так как коэффициент дифференцирования независимой переменной является соответствующей частной производной, * ) Заметим, что в предположении 1 О Дифференцируемости всех рассматриваемых признаков делается один и тот же вывод: valid. To для этого достаточно показать, что результат суперпозиции дифференцируемых функций также становится дифференцируемой функцией. Эти последние значения также получены. Например, если Q = ags12-напрямую сделать Х8 («у ди _ да _ _ х ВХ ~~ х ’+ г.

Смотрите также:

Решение задач по математическому анализу

Производные от сложных функций.	Применение полного дифференциала в приближенных вычислениях.
Полный дифференциал.	Однородные функции.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.