Интегрирование путем замены переменной

Оглавление:

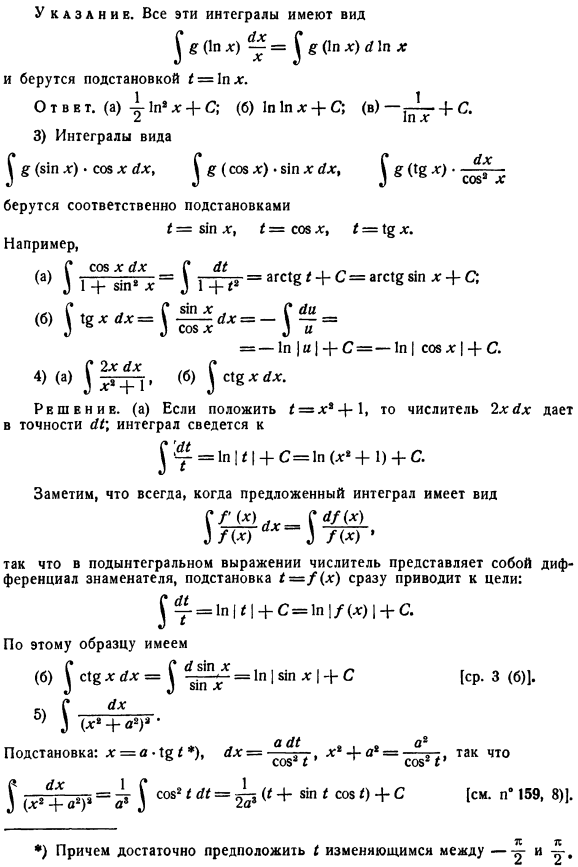
Интегрирование путем замены переменной

Интегрирование путем замены переменной. 1 из наиболее мощных способов интеграции функций, то есть представить метод или подстановку для замены variable. It основывается на следующих кратких замечаниях. $ ()»= 0()+С И затем… ())■> ’(■*)с1х=О(и>(х))+с. [Все функции, которые появляются здесь,§ ((), σ) (д), ж’ (^). предполагается, что она непрерывна] Это следует непосредственно из правила дифференцирования комплексной функции [Н°84]. О(совместно ( * )) = 0 (о.>(х)•со ’ ( * ) = 2 (0 (х)) ■ ко -（）、 0 ’（）= ^-（*）и если вы думаете. То же самое можно выразить по-разному, и соотношение таково м (о = ^(о ^ (согласно ww (Q)) также доступен[n°92]. Предположим, вам нужно вычислить Интеграл \ / (икс.) 。 Во многих случаях НН * = Вт (.Вы можете выбрать функцию типа () в качестве новой variable.

Подстановка может быть применена в другом формате, чем указанный. Людмила Фирмаль

So, подынтегральное выражение выражается следующим образом: f (x)ax = 2 (μ>(x)) ω ’(x), (1） Где(*) это/(.x) это хороший интерес. Тогда, как уже говорилось выше, достаточно найти Интеграл ^(0Л = 0(0 + с、 подставьте ^ = o> (^), чтобы получить Интеграл субъекта. Они обычно пишут кратко \ /(х) (1х = \ Е(1)-1, (2） Функция, представленная правым интегралом, уже подразумевает, что указанная подстановка имеет место. Например, найти Интеграл $ 3×3 * $ xyh. г $ 1П Х = y YX, поэтому установите я= ZX в X, чтобы преобразовать Подынтегральное выражение в следующую форму. 3!33 ^ потому что xyx=?Z1P8L / $ ЛН Х = П ( Х. Интегрирование последнего выражения легко вычисляется дружище = Т + с с! Просто вернуться к переменной X>вместо Н Х（：。 ля. Ж4 х. _ CN CNX потому что xyx = ^ [с.

Заметим, что при выборе подстановки* = о (Х) для упрощения подынтегральной функции необходимо помнить, что она должна включать фактор a>(х) 1x, который дает производную от новой переменной 11 (1)]. В предыдущем примере успех подстановки 2 = $ 1Н x определялся наличием фактора cos xyx = I. В этой связи показателен пример Здесь замените 1 = $ 1pd; потому что нет никакого фактора, упомянутого. Если вы попытаетесь извлечь из подынтегральной функции, то коэффициент$ т х YX или больше-shhhhhh, это будет подстановка * = ж $ д:; остальные выражения будут такими же. -$ 1P * LHvSOE * X-1 Эта замена упрощается. Тогда подмена оправдана у нас есть ^ = ^(-1) У = г-4-С = ^ Х — Х ГП 4С. То есть в подынтегральном выражении f (х) xx вместо x подставим функцию q; = Р (0) непосредственно из новой переменной I и получим выражение.

Очевидно, что в этом выражении замените/ = о(г), где o>(Т) является обратным от p ( * ), а затем вернитесь к исходному подынтегральному выражению f (х) 4x. So как уже упоминалось выше, уравнение (2) справедливо. На правой стороне, вы должны поместить = = RM (G). Найдите Интеграл, например.、 \ год О1-х ах. η= г 1 $ л).У нас есть а * —Х8 = а-ых СОА = а КНИ я У1 И затем ^ Г *-х * ух = а% ^ соз * я че Но мы уже знаем интегралы а * ^ с08 ** а = а * | г + −1 81P2 ^ + с {n * 159, 8)]. чтобы перейти к x, подставьте Г=асст -; преобразование пункта 2 облегчается следующим фактом: С ним 2 * = у а зт / * COS COS * г х у•х*. Один Один Два икс Наконец. Способность искать полезные заменители создается движением.

Вы не можете дать общих указаний по этому вопросу, но читатель найдет личные комментарии, которые облегчат этот поиск в следующем issue. In в случае канонического, замена просто указывается в курсе. Образцы. 1) (а) ^лилии% * xyh, Б)^• а)Рвшвнив. Верите ли вы, что? = х*, г(=2ххх, таким образом ^ Е * 1-xyx = ^ Е * А = Г?* + С = г б) Примечание. Та же замена. Ответ-agCT ^ x% 4 * CIn в обоих случаях Интеграл имел вид: Здесь—полезный для перестановки* = х *интеграция. икс Икс Функция для такого интеграла 2) (в)^ ^ ух, (б)^ Ага. х \ п * (Б） Я Ага. икс! Н * ДГ * = г ^ $(х ) ух. * ) уместно показать, что x будет меняться между-o и a, а я-будет меняться между-y и y. C в Канге. Все эти интегралы имеют следующий вид ^ ^ Р (1pl) НН Х.

Разность на квадрат под корнем (первая константа-константа) показывает тригонометрическую функцию подстановки. Людмила Фирмаль

Получается подстановкой* = 1plg. ,(А) г 1Н * х + с; (б) 1П х + С; © + С 3) отображение ^ ^ ($Ж-д)* С08 х уху ^ ^(С08 х)•5Вт х yx9 ^§(18 х)каждая перестановка будет принято Я = $ Ш x, 1 = С05 х, = х. Например тн1 АГС!§ / |С = ags12+с! 7. Соу х ых ы Да^ Тэд, ^ г ^ = =-1Н \ а -| -с-1Н | СОШ | -|-с. 4) (а) 1rtt-(б) ИК, е х Решение, (в) * = * * + 1, числитель 2ххх точно возвращает I1, а Интеграл равен Предлагаемые интегралы Ага. Я Г (х)SyX） / (икс） Три /（*）. ^ = 1пт + с = 1н (ХН-1) + с В подынтегральном выражении числитель является производной от знаменателя, и подстановка * = /(*) сразу приводит к цели. тн1 м = 1Н | * | + с = 1П | /(л:) 1 + с А это уже、 (б)^ с \% xc1x = ^ ^^ = 1Н | АП х \ + с [см. 3 (б)] 5）^（*■+ *）>• Замените X х = а \% 1 * \ ух = 5Т, ХС + а * = так °Соз * Я.

Таблица основных интегралов.	Интегрирование по частям.
Простейшие правила интегрирования.	Постановка задачи интегрирования в конечном виде.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.