Оглавление:
Подведение под знак дифференциала
По определению дифференциала:
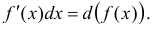
Переход в этом равенстве слева направо называют подведением множителя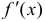 
под знак дифференциала.
Например:
Справедлива формула
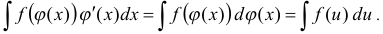
В данной контрольной работе составлены примеры на эту формулу в задаче 13(a).
Задача 13(a).
Найти неопределенные интегралы:
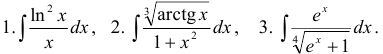
Решение:
1. 
.
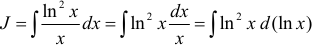Пусть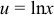 
, тогда 
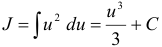. Переходя к первоначальной переменной 
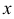, окончательно получим 
.
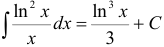Сделаем проверку: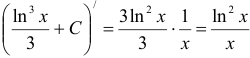 
это подынтегральная функция. Следовательно, интеграл вычислен верно.
Ответ: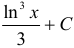 
.
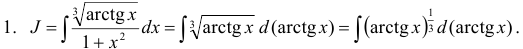
Здесь, очевидно,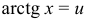 
. При некотором навыке замена функции через 
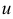обычно происходит устно.
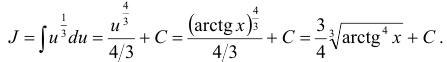
Ответ: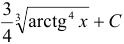 
.
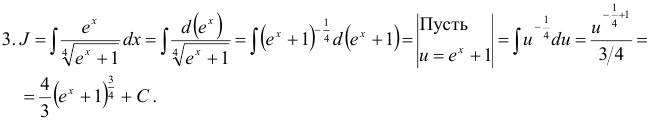
Ответ: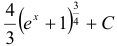 
.
Интегрирование по частям
Метод опирается на равенство
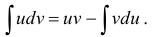
Для применения этого метода подынтегральное выражение следует представить в виде произведения одной функции на дифференциал другой функции. При этом целесообразно в качестве и выбирать функцию, упрощающуюся при дифференцировании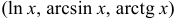 
.
Интегрированием по частям легко решаются интегралы вида:
Задача 13(б).
Найти неопределенный интеграл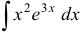 
.
Решение:
Все интегралы вычисляются с помощью интегрирования по частям:
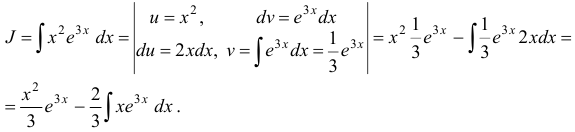
Для вычисления интеграла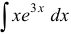 
применим еще раз интегрирование по частям: 
.
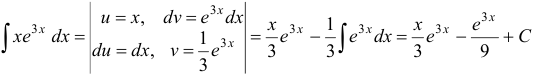Тогда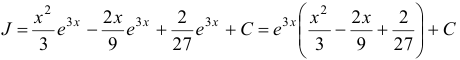 
.
Ответ: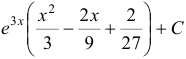 
.
Указания к решению задач
В предлагаемой литературе, приведенной в контрольном задании, подробно рассмотрены основные классы интегрируемых функций. Изучите примеры и методы их интегрирования.
В задаче 13(в) представлены интегралы вида:
которые легко свести к одному из табличных интегралов №16-21. Для этого необходимо уметь выделять полный квадрат из квадратного трехчлена:
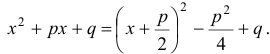
Задача 13 (в).
Найти неопределенный интеграл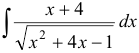 
.
Решение:
Выделим полный квадрат: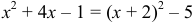 
.
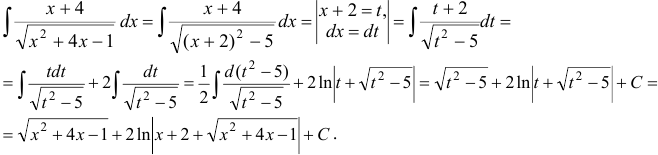
Задача 13(г).
Найти неопределенный интеграл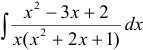 
.
Решение:
В задаче 13(г) используется схема интегрирования рациональных дробей. Дробь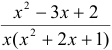 
рациональная, правильная (степень числителя меньше степени знаменателя), поэтому ее можно представить в виде суммы простейших дробей, а именно:
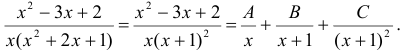
Приводя правую часть к общему знаменателю и приравнивая числители, получим тождество:
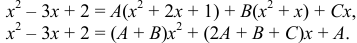
Коэффициенты при одинаковых степенях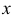 
в обеих частях тождества должны быть равны, поэтому получим систему уравнений
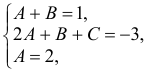
откуда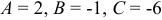 
.
Прием, с помощью которого найдены неизвестные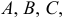 
называется способом сравнения коэффициентов.
Для определения коэффициентов часто бывает удобнее применить способ частных значений, состоящий в том, что после приравнивания числителей аргументам 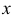придают некоторые удобные значения (читайте литературу).
Итак,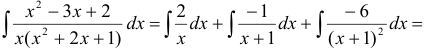 
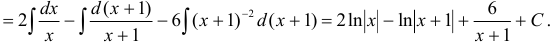
Ответ: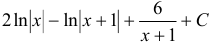 
.
Задача 13(д).
Найти неопределенный интеграл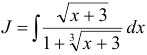 
.
Решение:
В задаче 13(д) представлен интеграл, который надлежащей заменой переменной может быть сведен к интегралам от рациональных функций.
Так как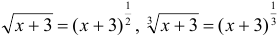 
, то наименьший общий знаменатель равен 6. Следовательно, сделаем замену:
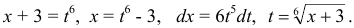
Тогда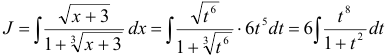 
.
Дробь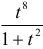 
рациональная, неправильная (степень числителя больше степени знаменателя), поэтому выделим целую часть:
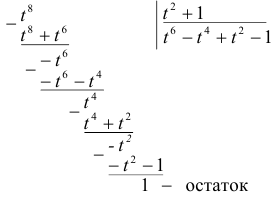
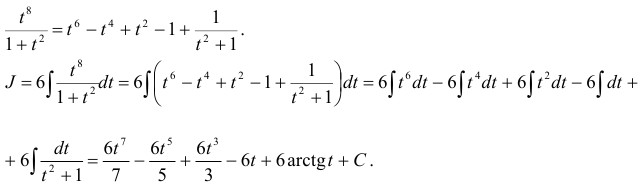
Перейдем к аргументу :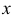
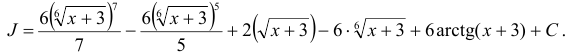
Ответ: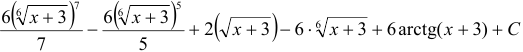 
В задаче 13(e) рассматриваются интегралы вида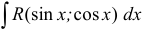 
, где 
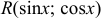— рациональная функция от 
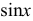и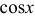 
. С помощью универсальной подстановки 
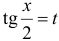интеграл сводится к интегралу от рациональной дроби нового аргумента 
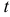. При такой подстановке:
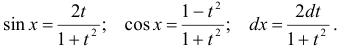
Замечание. Универсальная подстановка 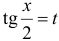нередко приводит к сложным выкладкам, поэтому изучите частные подстановки (читайте предлагаемую литературу).
Задача 13(e).
Найти неопределенный интеграл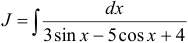 
.
Решение:
Используем универсальную подстановку 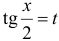, тогда
Перейдем к переменной :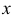 
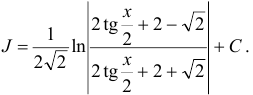
Ответ: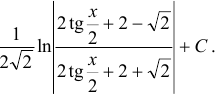 
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
