Не существует формулы, выражающей интеграл от произведения функций через интегралы от сомножителей. Но иногда интеграл от произведения функций можно вычислить по формуле интегрирования по частям.
Пусть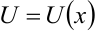 
и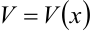 
— дифференцируемые функции. Тогда дифференциал произведения 
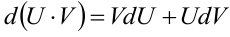. Проинтегрируем обе части формулы: 
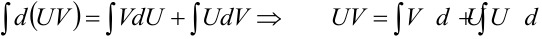. Окончательно, получим формулу
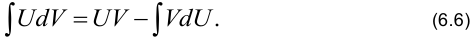
Формула (6.6) называется формулой интегрирования по частям.
Метод интегрирования по частям заключается в следующем.
Подынтегральную функцию исходного интеграла рассматриваем как произведение функции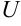 
и дифференциала некоторой функции 
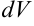. За дифференциал 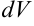мы должны выбрать выражение, для которого сможем найти первообразную.
После этого применяем формулу (6.6). Применять формулу имеет смысл в том случае, когда интеграл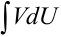 
окажется проще исходного или подобен ему.
Для получения окончательного результата иногда требуется применить метод последовательно несколько раз.
Пример 6.3 Найти интеграл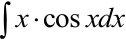 
.
Решение. Положим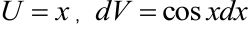 
. Тогда 
, 
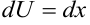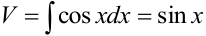. Произвольную постоянную учтем, когда получим первообразную для исходного интеграла. Применяем формулу (6.6):
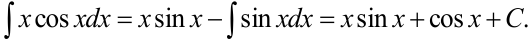
Методом интегрирования по частям вычисляются интегралы следующих типов (список интегралов можно расширить).
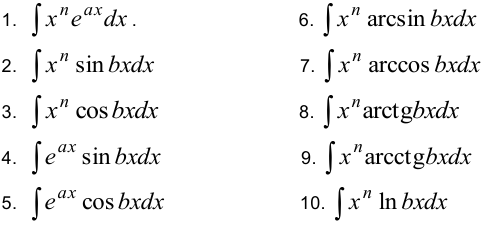
Примечания:
1) в интегралах 1, 2, 3 за функцию 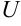следует принимать 
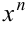(вместо сомножителя 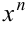в интеграле может стоять многочлен по степеням 
);
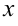2) в интегралах 6 — 10 следует принять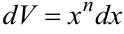 
, за функцию 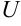принять все, что остается в подынтегральном выражении;
3) в интегралах 4, 5 безразлично, что принимать за 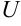, но формула применяется дважды.
Последнее примечание рассмотрим на примере.
Пример 6.4 Найти интеграл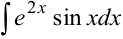 
.
Решение. Обозначим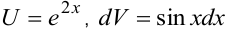 
. Тогда 
, 
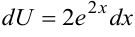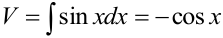. Применяем формулу интегрирования по частям:
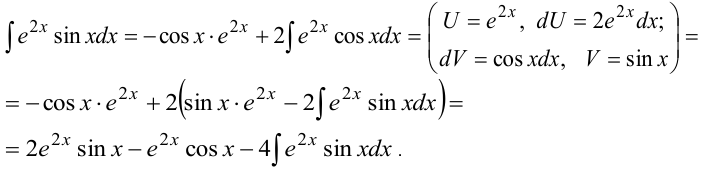
Таким образом, после двукратного применения формулы в правой части появился исходный интеграл:
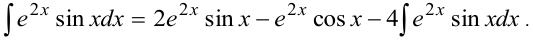
«Интеграл вернулся». Его и называют «возвратным». Получили уравнение относительно исходного интеграла. Перенесем «возвратный» интеграл в левую часть.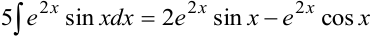 
. Окончательно, прибавив произвольную постоянную, получим:
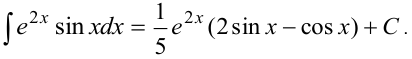
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Первообразная. Неопределённый интеграл и его свойства |
| Таблица интегралов и табличное интегрирование |
| Интегрирование подстановкой |
| Интегрирование простейших рациональных дробей |
