Оглавление:
Рассмотрим нахождение неопределенных интеграл от следующих типов иррациональных функций: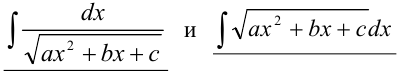 
(
— 
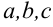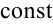). Для их нахождения будем использовать метод выделения полного квадрата в иррациональном выражении. Тогда рассматриваемые интегралы можно будет привести к видам:
,
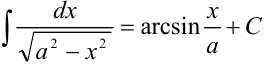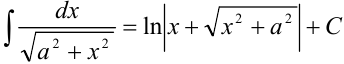или
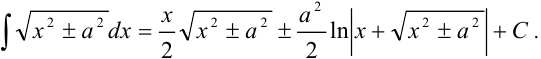
Разберем нахождение интегралов от некоторых иррациональных функций на конкретных примерах.
Пример №20.4.
Найдите интеграл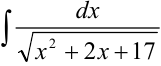 
.
Решение:
Попытаемся выделить в знаменателе полный квадрат. Для этого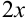 
представляем как удвоенное произведение 
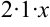. Тогда к выражению 
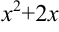следует добавить квадрат единицы 
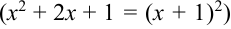и вычесть 1. Получим цепочку преобразований:
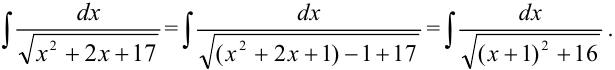
Вычислим полученный интеграл методом подстановки. Положим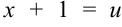 
, тогда 
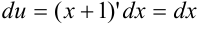. Подставим 
, 
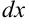в полученный интеграл: 
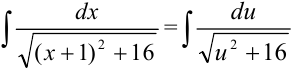. Воспользуемся табличным интегралом: 
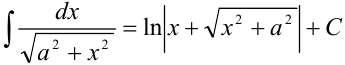, где 
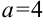. Получим, что 
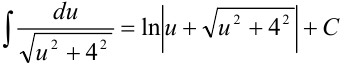. Подставим вместо выражение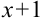 
:
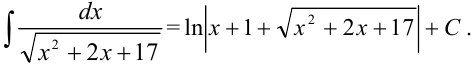
Ответ: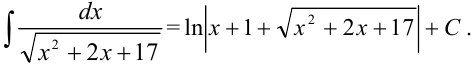
Пример №20.5.
Найдите интеграл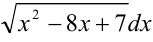 
.
Решение:
Попытаемся выделить под знаком корня полный квадрат. Для этого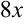 
представляем как удвоенное произведение 
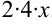. Тогда к выражению 
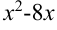следует добавить квадрат четырех 
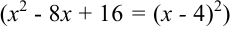и вычесть его. Получим цепочку преобразований:
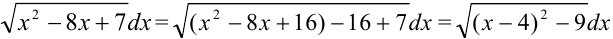
Вычислим полученный интеграл методом подстановки. Положим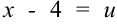 
, тогда 
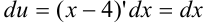. Подставим , 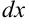в полученный интеграл: 
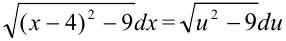. Воспользуемся табличным интегралом: 
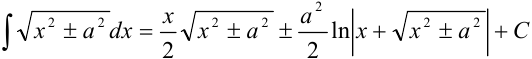, где 
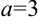. Получим, что 
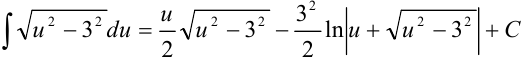. Подставим вместо выражение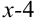 
:
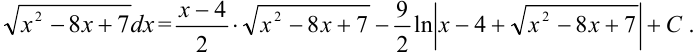
Ответ:
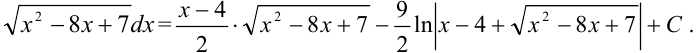
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Метод интегрирования по частям. |
| Интегрирование простейших рациональных дробей. |
| Универсальная тригонометрическая подстановка. |
| Понятие определенного интеграла. |
