Оглавление:
Вычислить заданный интеграл непосредственным интегрированием или взятием его как интеграла от некоторой сложной функции удастся далеко не всегда. Одним из наиболее эффективных приемов является метод подстановки. Сущность этого метода заключается в том, что путем введения новой переменной удастся свести заданный интеграл к новому интегралу, который чаще всего является табличным.
В основе метода подстановки лежит утверждение, являющееся следствием правила дифференцирования производной сложной функции. Пусть задана сложная функция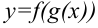 
. Тогда исходный интеграл можно привести к виду: 
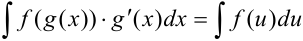. Эта формула называется формулой замены переменных в неопределенном интеграле.
Приведем алгоритм нахождения неопределенного интеграла методом замены переменной.
- Введем новую переменную
таким образом, чтобы под знаком интеграла стояла функция, содержащая , и производная (
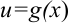). - Найдем
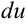по формуле: 
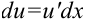. - Выразим
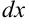через 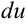(при этом помним, что если множитель в одной части формулы находился в числителе, то в другую часть он перейдет в знаменатель и наоборот: если множитель находился в знаменателе, то в другую часть он перейдет в числитель). - Подставим и 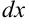в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной :
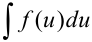. - Вычислить интеграл с переменной .
- Перейти от переменной интегрирования к исходной переменной
.
Рассмотрим применение метода подстановки на конкретных примерах.
Пример №19.8.
Найдите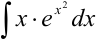 
.
Решение:
1. Выполним подстановку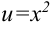 
с целью прийти к интегралу от функции 
.
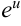2. Найдем 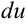по формуле : 
.
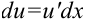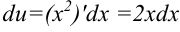3. Выразим 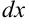из выражения пункта 2 
.
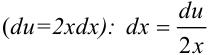4. Подставим и 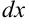в исходный интеграл: 
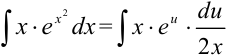. Видим, что можно сократить и прийти к интегралу относительно переменной : 
.
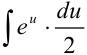5. Для нахождения полученного интеграла константу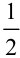 
вынесем за знак интеграла: 
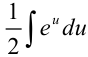. По таблице неопределенных интегралов находим, что 
.
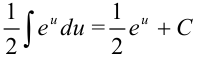6. Поскольку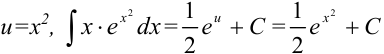 
.
Ответ: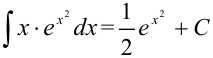 
.
Пример №19.9.
Найдите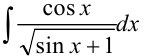 
.
Решение:
1. Выполним подстановку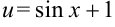 
. Тогда под знаком интеграла будет стоять функция от 
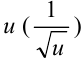и производная 
.
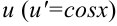2. Найдем 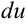по формуле : 
.
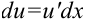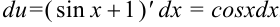3. Выразим 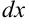из выражения пункта 2 
.
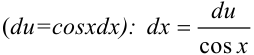4. Подставим и 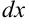в исходный интеграл: 
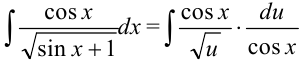. Видим, что 
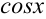можно сократить и прийти к интегралу относительно переменной : 
.
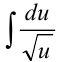5. По таблице неопределенных интегралов находим, что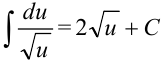 
.
6. Поскольку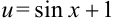 
, 
.
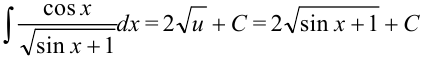Ответ: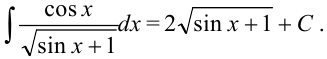 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Непосредственное интегрирование. |
| Интегралы от некоторых сложных функций. |
| Метод интегрирования по частям. |
| Интегрирование простейших рациональных дробей. |
