Оглавление:
Интегрирование иррациональных функций
Обозначим через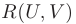 
функцию переменных 
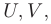которая построена с использованием только четырех арифметических действий 
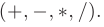. Интегралы вида 
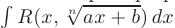сводятся к интегралу от рациональной функции 
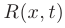с помощью подстановки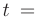 
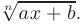
Пример:
Найти неопределенный интеграл от иррациональной функции
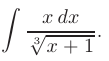
► Рационализируем подынтегральную функцию подстановкой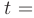 
:
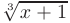Интегрирование некоторых тригонометрических функций
Интегралы вида
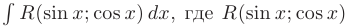
рациональная функция тригонометрических аргументов, сводятся к интегралу от рациональной функции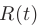 
с помощью так называемой универсальной тригонометрической подстановки
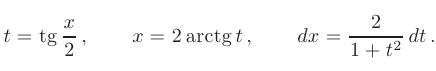
Выражая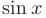 
и 
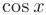через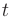 
, получим:
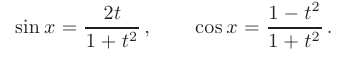
Заметим, что универсальная подстановка часто приводит к слишком сложным рациональным дробям. Поэтому полезно выделить несколько частных случаев, допускающих использование более простых тригонометрических подстановок:
а) если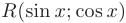 
— функция, нечетная относительно : 
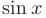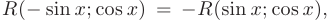, то в качестве подстановки следует использовать 
;
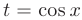б) если 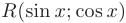— функция, нечетная относительно : 
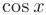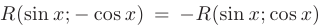, то в качестве подстановки следует использовать 
;
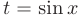в) если 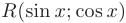— функция, четная относительно 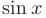и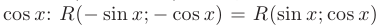 
, то в качестве подстановки следует использовать 
.
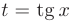Интегралы вида
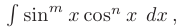
где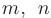 
— целые неотрицательные числа, сводятся к интегралу от рациональной функции с помощью следующих тригонометрических подстановок:
а) если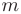 
— нечетное, то в качестве подстановки следует использовать ;
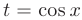б) если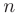 
— нечетное, то в качестве подстановки следует использовать ;
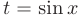в) если 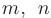— четные, то следует использовать следующие тригонометрические формулы для понижения степени:
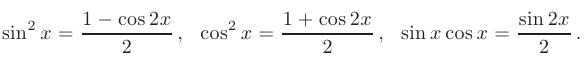
- Интегралы вида
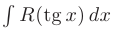приводятся к интегралу от рациональной функции с помощью замены:
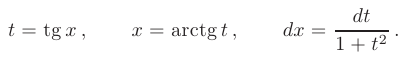
- Интегралы от произведения тригонометрических функций различных аргументов приводятся к интегралу от алгебраической суммы соответствующих функций с применением следующих формул:
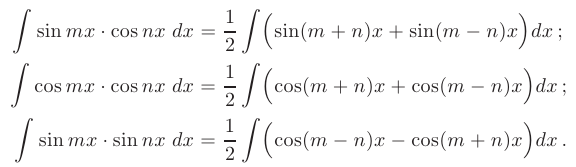
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Интегрирование некоторых классов функций в математике |
| Интегрирование рациональных дробей в математике |
| Понятие определенного интеграла в математике |
| Понятие о несобственных интегралах в математике |
