Интегральный признак Маклорена-Коши

Оглавление:

Интегральный признак Маклорена-Коши

Интегральный признак Маклорена-Коши. В заключение мы выводим еще одну функцию 1, которая отличается по форме от всех предыдущих. Пусть предлагаемый ряд имеет следующий вид ！> » =![] / («). (5） I-1 Нет.■） Где f(x) значение при x = n некоторой функции f (x)>, определенной для этой функции. Положительный и монотонный спад. рассмотрим некоторые примитивные функции f (x). р(х)= ^ /(х) х. Его производная P ’(g) /(g:) равна 0, поэтому P (x) увеличивается вместе для x и x-°C предел, вероятно, конечен или нет[n°47].И различие между этими случаями основано на следующих признаках конвергенции и дивергенции: это было выражено геометрически Маклореном еще в 1742 году, но не было замечено и возобновлено Коши в 1827 году. Неотъемлемый атрибут. Ряд (5) сходится, когда предел/обратной производной P (x) конечен, и расходится, когда/,= oo.

Начальным значением n вместо 1 может быть любое другое натуральное число, n0. Людмила Фирмаль

Функция f (x) также должна быть рассмотрена * Р (х)= $ /(х） Да. (6） Учитывая монотонность функции f (x:), если n ^ x ^ n-1-1 ay + 1 = / («+1X/（*）» /（ «）= а、 л + 1 Так… Но… л + 1 топор ^ АП | | / / (х). н. О номере л + 1 ^ ] / (х) ЛК 1-литровый Очевидно, что не имеет значения, о каких антипроизводных идет речь. И это неудивительно, ведь 2 антипроизводных отличаются только своей константой. Поставь л Количество части Ясно, что этот ряд сходится или расходится точно в зависимости от того, является ли b конечным. Используя конечное A, «теорема сравнения» 1 [n°237]также сходится к ряду меньших членов. И 2X + 1, линия asni (5); напротив, 1 =1°, еще чаще И Серия с более крупными членами: 2 ap, или Серия(5). Один Пример 1) сначала снова рассмотрим все гармонические ряды. Так 00 2тг> Б> 2 * л = 1 л = 1 Дело(а)： /()=-^ р, п(х) = ^ ^ = 1П п:-оо для Q-ОО、 Линия разветвится. b) дело： ПХ） = Р. ？() = §%7 = для q: -.°、 Линии сходятся.

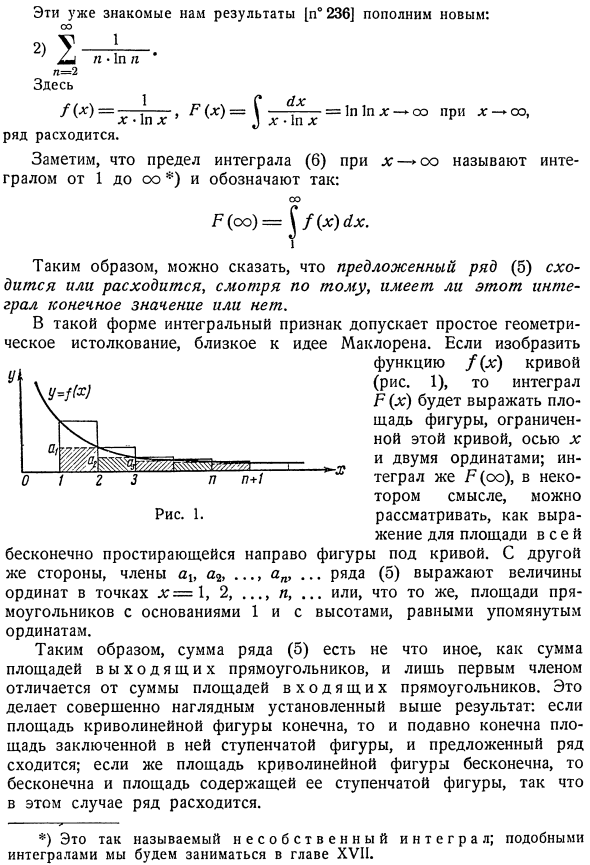
Пополните эти уже знакомые результаты (pv236) новыми. И н = 2 Здесь. 2)2 л■1П Н• = 2 Кб /(dg)= rn1rr ^(LH)= 1ZGTTG = 1n1pds-00 «P»* °Линия разветвится. это называется ОО. Обратите внимание на ограничение интеграла (1〜oo) от x с границами (6), выраженное следующим образом: Да. п(оо)= ^ /(х) х. Таким образом, можно сказать, что предлагаемый ряд (5) сходится или расходится в зависимости от того, имеет ли этот Интеграл конечное значение или нет. В таком виде интегральная функция находит простую геометрическую интерпретацию, близкую идее Маклорина. Когда изображать функция? для кривых (x) (Рис. 1) Интеграл P(. 😉 Представляет собой область этой кривой, ось x и фигуру, заключенную в 2 вертикальных coordinates. In в некотором смысле.

Интеграл P (oo)} можно рассматривать как выражение площади всей фигуры, которая бесконечно простирается до нижнего правого угла кривой. Людмила Фирмаль

С другой стороны, термин a B a в ряду (o)…Ан> …Точки η= 1, 2, … n,…представляют собой вертикальную координату объекта, при этом площадь прямоугольника равна высоте основания 1 и указанной выше ординате. Следовательно, сумма ряда(5) является только суммой Исходящая прямоугольная область, и только первый элемент Он отличается от суммы площади входящего прямоугольника. Это делает приведенные выше результаты очень ясными. Если площадь криволинейной фигуры конечна, то площадь ступенчатой фигуры, окруженной ею, конечна, и предлагаемый ряд сходится. Если площадь криволинейной фигуры бесконечна, то площадь ступенчатой фигуры, содержащей ее, также бесконечна, поэтому в этом случае ряды расходятся. *) Это так называемый неправильный Интеграл. Такой Интеграл описан в главе XVII.

Признаки Коши и Даламбера.	Принцип сходимости.
Признак Раабе.	Абсолютная сходимость.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.