Оглавление:


Интеграл и задача об определении площади
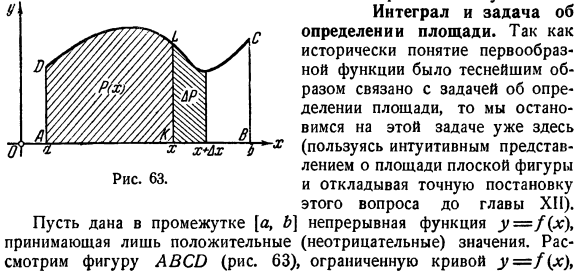
Интеграл и задача об определении площади. Рассмотрим рисунок ABCO (рисунок 63) в интервале[a, b], который принимает только положительные значения. Интегралы и задачи для определения площади. (используем интуитивное представление о площади в плане и откладываем точную формулировку этого вопроса до XII главы).Непрерывная функция y =./(x (неотрицательное) значение. Кривой Y = F (х)、 2. с двумя ординатами X = a и x = b и сегментами оси x аналогичная фигура называется криволинейной trapezoid.
Исторически понятие контрдифференциальной функции тесно связано с проблемой определения площади, поэтому здесь мы уже описываем эту проблему. Людмила Фирмаль
- To определив область р этой фигуры, мы изучаем поведение области переменной Aky фигуры в ординате, которая соответствует начальной ординате x = a и произвольно выбранному значению x в интервале[a, b]. когда x изменяется, эта последняя область изменяется соответственно, и каждый x имеет четко определенное значение, поэтому изогнутая трапециевидная L / C x / E область становится функцией X. Она представлена P (x). Во-первых, мы ставим задачу найти производную этой функции. Для этого, если вы дадите x (положительное) приращение Ддг, то область P (X) получит приращение GR. Минимальное и максимальное значения f (x) в интервале[x> x-\ Dd:) [N°73]представлены соответственно m и VL, а площадь DG сравнивается с площадью прямоугольника, построенного на основе Dd.
И высоты т и М / I DD; DR L1 DDG、 Откуда Т ^ Х М Для Dx > 0, M и M имеют тенденцию быть f ( * ), из-за непрерывности、 Р ’(х)= ЕСВ ^ = /(). Итак, обычно мы доходим до известной теоремы, называемой Теоремой Ньютона и Лейбница): производная переменной области P (x 🙂 относительно конечной абсциссы становится равной конечной ординате y = f(x). То есть переменная область P (x) является примитивной функцией заданной функции y = f(x).Среди других примитивов эта обратная производная отличается знаком, что она исчезает с x = A. So, обратный дифференциал P (x) известен о функции f (x), а по теореме предыдущего числа Р(х)= П(Х)+ с、 Константу C можно легко определить, установив здесь x = a. 0 = р(а)+C.
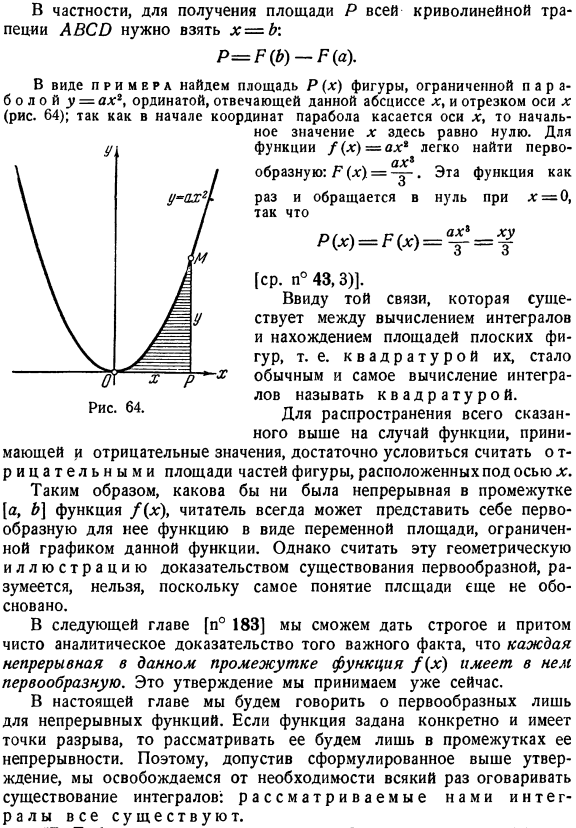
- Таким образом, С—Р(А). Наконец. Р(х)= р(х) р(а). * ) На практике это предложение было опубликовано Исааком Барроу (1630-1677), учителем из Ньютона (хотя и в другой форме). В частности, чтобы получить площадь P всей кривой трапеции ABC, x = b \ Р = р(в) р(а). В качестве примера найдем область P (x) фигуры, ограниченную параболой y = ahg, ординату, соответствующую заданной абсциссе qg, и отрезок оси x (рис.64).Начальное значение x равно нулю, потому что она касается оси Х в начале координат параболы. Легко найти первый Соотношение рис.: / 7 (g)= -^ -.Эта функция является исчезают при η = 0、 Р(х)= р (х)= А4 = ч [ср. Н°43.3)].
Стало общепринятым называть вычисление интеграла квадратурой, принимая во внимание связь, существующую между вычислением интеграла и нахождением площади плоской фигуры, то есть их квадратуры. Чтобы распространить все вышесказанное на случай функции, принимающей отрицательное значение, достаточно рассмотреть площадь части фигуры под осью x как отрицательную. Таким образом, даже если функция/(*) непрерывна на интервале[a, b], читатель всегда может представить для нее контрдифференциальную функцию в виде переменной области, ограниченной графом этой функции.
Однако эту геометрическую фигуру нельзя рассматривать как доказательство существования антидифференциала, поскольку само понятие этой области еще не было продемонстрировано. Людмила Фирмаль
- В следующей главе [n°183] мы можем дать строгое, но чисто аналитическое доказательство важного факта, что все функции P (x), которые смежно содержат примитивы. Теперь примите это утверждение. В этой главе описаны контр-производные только непрерывных функций. Если функция конкретно задана и есть точка останова, рассматривайте ее только в своей непрерывности interval. So, если мы признаем вышеизложенное утверждение, то каждый раз мы свободны от необходимости оговаривать существование интеграла. Все интегралы, о которых мы думаем, существуют.
Смотрите также:
Решение задач по математическому анализу
| Наибольшее и наименьшее значения функции. Примеры. | Таблица основных интегралов. |
| Понятие первообразной функции (и неопределенного интеграла). | Простейшие правила интегрирования. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

