Идеальный газ

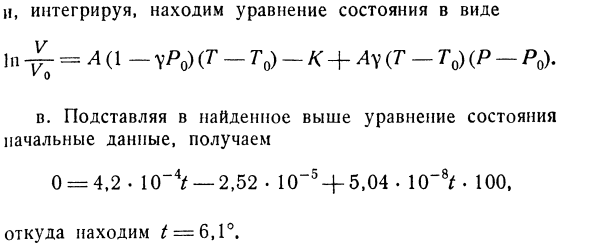
Идеальный газ

• Образцы 1.Идеально gas. As в качестве первого примера рассмотрим известное уравнение состояния идеального газа ФВ = Р(Т + 273.15), (1.2） Где T-температура в градусах Цельсия. В этом масштабе температура плавления льда равна 0°C, а температура кипения воды-100°C (как при нормальном атмосферном давлении 760 мм рт. ст.). На 1 моль, газовая постоянная равна Я = 8.314. 107 эрг / град = 1,986 кал / град. (1.3） x) шкала абсолютных температур была

принята в 1954 году на 10-м весоизмерительном совещании. На этой шкале фиксируется только 1 балл на шкале. Или 0,01°C. In по обычной стоградусной шкале, описанной в тексте, температура тройной точки воды составляет 0,0098°С, поэтому разница между обеими шкалами невелика и обычно незначительна. Температура идеальной газовой шкалы определяется следующим образом: 7 = ^ + 273.15°. Введение этой переменной в уравнение состояния является знакомой

формой ФВ = РТ. (1.4） Иногда удобнее относить количество, включенное в это уравнение, не к 1 молю вещества, а к 1 molecule. In в этом случае уравнение состояния записывается следующим образом: ПВ = кт,(1.5） Куда? В. v = — DG-удельный объем за счет 1 молекулы、 R 0,6) K = — JJ постоянная больцмая、 N = 6.023 ″ 1023-это число Авогадро. Если уравнение содержит только

Уравнение состояния может быть геометрически описано различными способами. Людмила Фирмаль

3 переменные и записано в виде/(H, 7 \ V)= 0, то в качестве оси декартовой системы координат плоскости можно выбрать любую из этих 2 (например, P и V).Тогда при фиксированном значении 3-й переменной, Т, уравнение состояния определяет кривую на этой плоскости. Для идеального газа эта кривая является константой гиперболического PV-планарного PV. Если запустить эти кривые при разных температурах ТВ Т2, то получится семейство кривых с разными значениями параметра 7.Эти кривые называются

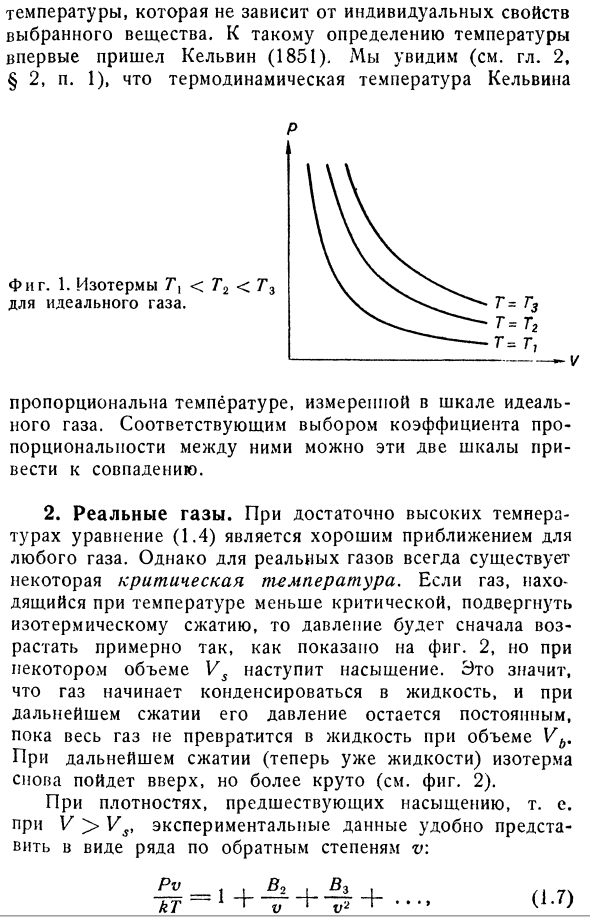
изотермами.式（１．Изотермический идеальный газ, описанный четвертым) показан на фиг. 1.Реальные газы, такие как гелий и водород при низком давлении, следуют этому уравнению состояния очень well. So, предполагая, что температура равна PV / R вдоль Изотерм 1 моля газа, можно ввести шкалу температуры идеального газа. Однако, как уже упоминалось во введении, термодинамическая шкала вводится с использованием второго закона термодинамики Температура не зависит от индивидуальных особенностей выбранного материала. Кельвин(1851)впервые достиг определения этой температуры. Термодинамическая температура Кельвина (гл.2,§ 2, стр. см. 1） П. С. Она пропорциональна температуре, измеренной на идеальном газе scale. By правильно подобрав

коэффициент пропорциональности между ними, не исключено, что эти 2 шкалы совпадут. 2.Реальный газ. Для достаточно горячего тура формула (1.4) является приближением, подходящим для любого газа. Однако для реальных газов, всегда существует некоторая критическая температура. Когда газ с критической температурой подвергается изотермическому сжатию, давление сначала увеличивается примерно так, как показано на рис.3. 2, но в определенном объеме Vs происходит насыщение. Это означает, что газ начинает

• конденсироваться и становиться жидким, и тем более при сжатии его давление остается постоянным до тех пор, пока все газы не станут объемом VB жидкости. При дальнейшем уплотнении (теперь жидком) изотерма снова поднимается, но более резко (см. Рисунок 2). Для плотности, предшествующей насыщению, то есть V> Vs, удобно представить экспериментальные данные в виде ряда обратной мощности V. Где коэффициент B {зависит от температуры. Камерлинг-Оинс ввел этот метод в 1902 году. Вы можете быть удовлетворены тем,

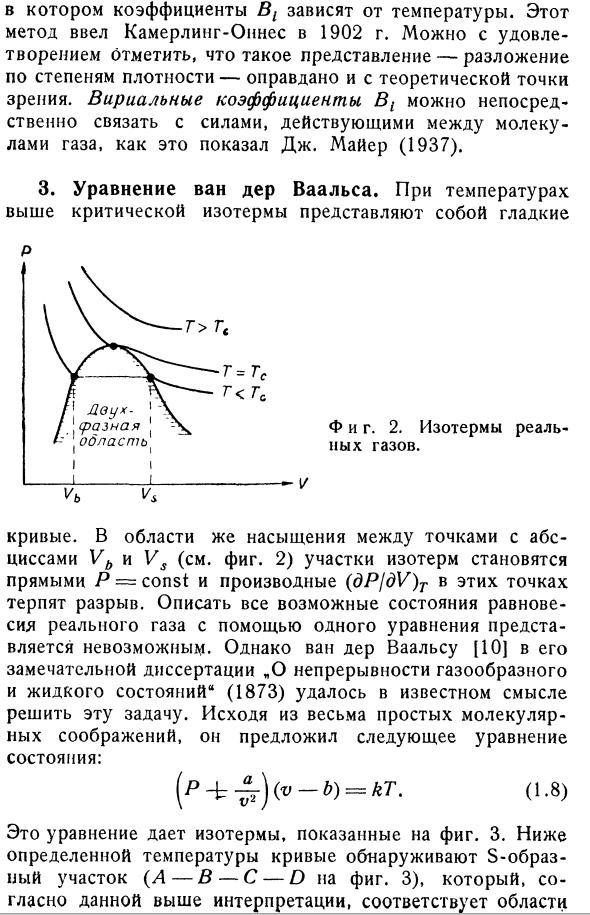
что такое выражение (расширение мощности плотности) также оправдано с теоретической точки зрения. Вириальный коэффициент B1 равен J. As указанная Майером (1937), она непосредственно связана с силами, действующими между молекулами газа. 3.. At температура выше критической изотермы, она гладкая П. С. г = ГФ г <ГФ И фигура тоже. 2.Изотермы реальных газов. VB против The curve. In в насыщенной области (см. Рис. 2), где абсцисса находится между точками Vb и Vs, сечение Изотерм становится прямой P-const, а производная (dPjdV) T в этих точках является разрывной. Используя одно уравнение, кажется

Уравнение Ван Дера Waals Людмила Фирмаль

невозможным описать все возможные состояния равновесия существующего газа. Ван дер Ваальс [10], однако, так или иначе решил эту проблему в своем замечательном трактате»непрерывность газообразного и жидкого состояний»(1873).Основанный на очень простых молекулярных соображениях、 (П-Т <α-б)= БТ — (1.8） Это уравнение дает изотермы, показанные на фиг. 方程式温線は この、さ 図２の さ的 さ温 さの さ さ的 さ さを さえる。 3.Ниже определенной температуры кривая показывает S-образную область (A-B-C-D На рисунке 3).Это, согласно приведенной выше интерпретации,

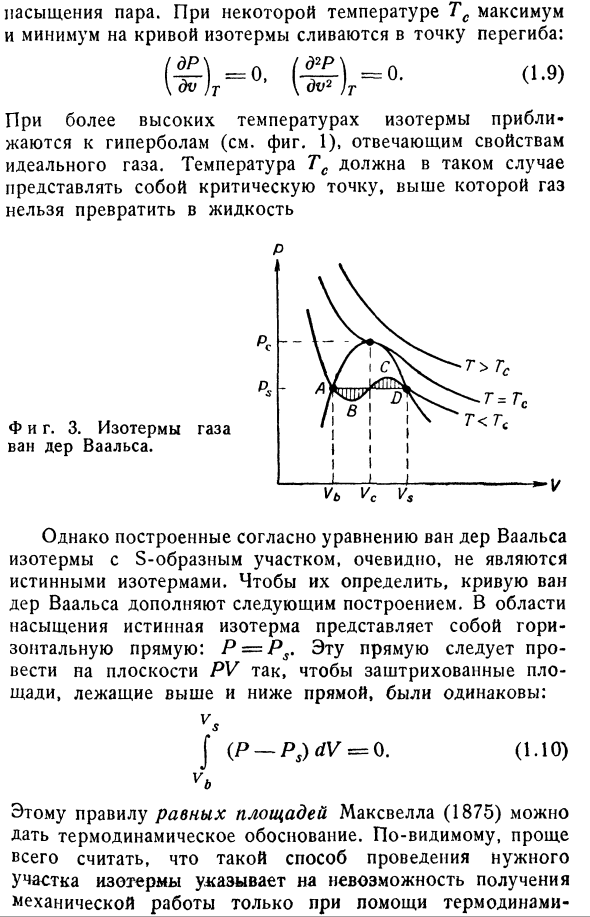
соответствует его территории Пар saturation. At определенная температура Tc, максимальное и минимальное значения кривой изотермы объединяются в точке перегиба. При высоких температурах изотерма приближается к гиперболе, что соответствует характеристике идеального газа(см. Рис. 1).Температура Tc, когда она превышена, должна сделать газ критической точкой. Нельзя превратить в жидкость С. С. И фигура тоже. 3. Ван-дер-ваальсовы

изотермы газов. Однако изотермы S-образного участка, построенные по уравнениям Ван-дер-Ваальса, явно не соответствуют действительности isotherms. To для их определения к кривой ван-дер-Ваальса были добавлены следующие структуры: в насыщенной области истинными изотермами являются горизонты P = PS. Эта линия должна быть нарисована на плоскости PV так, чтобы

заштрихованные области выше и ниже линии были одинаковыми. Дж(П-ПС)дв =0.(1.10） vt. Этому правилу равной площади Максвелла (1875) можно дать термодинамическое обоснование. Очевидно, проще всего предположить, что такой способ проведения искомой части изотермы указывает на невозможность получения механической работы только с помощью термодинамики. Цикл 1) состоящий из S-образной части и горизонтальной линии. Разделы A-B и C-D, где

давление»ниже давления насыщения пара«и выше, также могут иметь дату. Это особый случай explanation. It характеризуется как состояние перегретой жидкости и пересыщенного пара. Однако эти состояния не являются устойчивыми равновесными состояниями термодинамической фазы. Конкретное возражение может быть вызвано сечением B-C, которое соответствует снижению давления при сжатии. Простое рассуждение предполагает, что такое состояние

не может находиться в равновесии. Условия устойчивости термодинамической системы мы рассмотрим позже (см. Главу 3,§ 6).Один из них описывается в виде (dPldV)T <0 и нарушается в S-образной области. Тем не менее уравнения Ван-дер-Ваальса, дополненные правилами Максвелла (1.10), показывают качественно правильную ситуацию сложного явления, если не учитывать

окрестности критической точки (см. Приложение в).Согласно теории Ван-дер-Ваальса, область двухфазной системы (жидкость и ее насыщенный пар) ограничена параболической кривой, проходящей через критическую точку, как показано на рисунке 1. 3.Однако верно ли это во всех деталях, также пока нельзя сказать с полной уверенностью. В дополнение к этим кратким сведениям об уравнении ван-дер-Ваальса константы a и b указывают только

на то, что связь может быть связана с важными параметрами газа. ПСК = беспроводным доступом; — ВК =™т> — на） (1.8) и сразу следует из (1.9). в теории Ван-дер-Ваальса соотношение важных параметров имеет универсальное значение: PcVcjRTc = 3/8.как показал эксперимент, для нормальных газов это соотношение находится

в диапазоне 0,2-0,3. Я asked. In область насыщения, Vb <V <Vv (см. Рис. 3), указывает на то, что точка V разделяет горизонтальную часть Изотерм 1) для доказательства правила Максвелла см., например, [36]. С. С. 194.- ОПри соотношении, равном соотношению молей в паровой фазе и в жидкой фазе. Решение, общее количество молекул равно сумме количества молекул в обеих фазах. СП = А / Т + / В2. на VX

и V2 представляют собой удельный объем на молекулу газа и жидкости、 Vb = Nv2, V = Nxvx + N2v2, = Nvv. В-глаг _ N Т ВС-в — ’г’ Если вам нужно доказать. Интересно рассмотреть следующие эксперименты. Если жидкость нагревается в герметичных ампулах (tube de la Tour), то согласно приведенной выше теории, необходимо соблюдать только 2 возможности (см. Рисунок 2). 1. V <V s. мениск,

отделяющий жидкость от пара, поднимается до тех пор, пока вся ампула не заполнится жидкостью. 2. В ВК. Мениск опускается до тех пор, пока вся жидкость не испарится. Однако ситуация, которая наблюдается на практике, не столь однозначна defined. It известно, что если объем жидкости приблизительно равен критическому, то мениск останется на некоторое время, и можно наблюдать, как

мениск разрушается, когда система проходит через критическую температуру. При определенных условиях также можно наблюдать очень красивое явление диффузного рассеяния света (критический молочный свет). Таска. Gas der der Waals выводит зависимость между коэффициентом теплового расширения и степенью сжатия газа. (Среди задач, предложенных на экзамене Оксфордского университета

1962 года） а. уравнение состояния и коэффициенты жидкости со степенью сжатия[1 +Щ7\ — Т0) Тепловое расширение a = A(1-y R), где / C = 2.52•10 «„5 атм — \ p = = 2.10“ 3 градуса — \Г0= 273°K. A = 4.2•10-4 градуса » 1, y = 1-2 * 10 ^ 4 атм ’\ c. жидкость сначала заполняет контейнер, где давление равно 0, а температура Г0= 273°.Сколько раз мне нужно поднять температуру, чтобы увеличить давление до 100 атмосфер? (Среди заданий, предусмотренных на экзамене

Оксфордского университета 1961 г.） Решение проблемы a. By определение、 1 (dU \ 1 (dU \ a = — v (w)P и H = = — YYG- Из уравнения Ван-дер-Ваальса дю _ RHV-б)ГВ _ Б-В дю dT — [RT 1 (V-b)2-2π/ V3] ’ dP-R dG 9 Следовательно、 А _ Р К U-b• Эта связь является частным случаем общей формулы a. потому что я знаю производные — РИЧ-О-Л И = ^(1 + п(71-7 * о) 1. Вы можете найти общую производную d InV. Получаем

отношение Lu = / Cp из интегрируемого условия всей производной. Этому отвечает число, указанное в условии задачи. Следовательно、 D В В А (1-гг) ДТ-{к + Айо ДП Затем интегрируем и находим уравнение состояния в виде — £- =А (- yP0)(Т-т0) — к + Ау(Т-т0)(Р-Ро).Вы c. подставляя исходные данные в приведенное выше уравнение состояния, получаем следующее 0 = 4.2•10-4 /-2.52•1（Т5 +5.04.Вы найдете 10-8t-100 и^ = 6.1°оттуда.

Смотрите также:

Предмет термодинамика

Тройные системы	Внутренняя энергия
Термодинамическое состояние	Обратимые процессы