Оглавление:
Для решения задач линейного программирования разработано множество методов, но наиболее популярными из них являются графический, симплексный и двойственный методы, которые мы и рассмотрим далее в нашей исследовательской работе.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Возможно эта страница вам будет полезна:
| Предмет математическое программирование |
Графический метод решения задач линейного программирования
Рассмотрим задачу линейного программирования в стандартной форме записи с двумя переменными
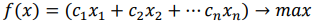
при условиях:
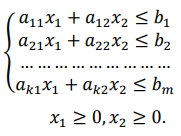
Необходимо найти вектор 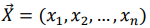 , удовлетворяющий данной математической модели.
, удовлетворяющий данной математической модели.
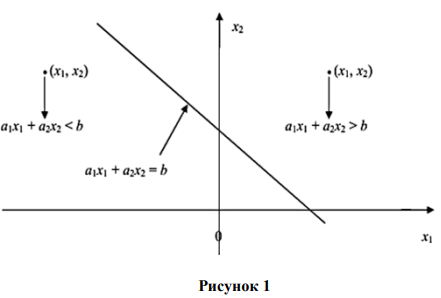
При решении, прежде всего, необходимо найти область допустимых решений системы неравенств (3.2). Рассмотрим декартову систему координат  . Заменив каждое из неравенств (3.2) равенством, строим соответствующую ему граничную прямую
. Заменив каждое из неравенств (3.2) равенством, строим соответствующую ему граничную прямую 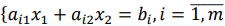 . На рисунке 1 видно, как эта прямая делит плоскость
. На рисунке 1 видно, как эта прямая делит плоскость  на две полуплоскости [3].
на две полуплоскости [3].
Чтобы определить, какую именно полуплоскость определяет данное неравенство, достаточно взять произвольную точку плоскости ( ) (например, начало координат) и подставить в неравенство числа
) (например, начало координат) и подставить в неравенство числа 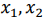 . Если оно удовлетворится, то полуплоскость, в которой лежит данная точка — искомая. В противном случае нужная полуплоскость лежит по другую сторону прямой
. Если оно удовлетворится, то полуплоскость, в которой лежит данная точка — искомая. В противном случае нужная полуплоскость лежит по другую сторону прямой  [26].
[26].
Для нахождения области допустимых решений строим граничные прямые полуплоскости, соответствующие всем неравенствам. Общая часть («пересечение») всех этих полуплоскостей будет решением системы неравенств данной задачи.
При нахождении области допустимых решений (ОДР) задачи линейного программирования может встретиться один из четырех случаев, рассмотренных в таблице 4:
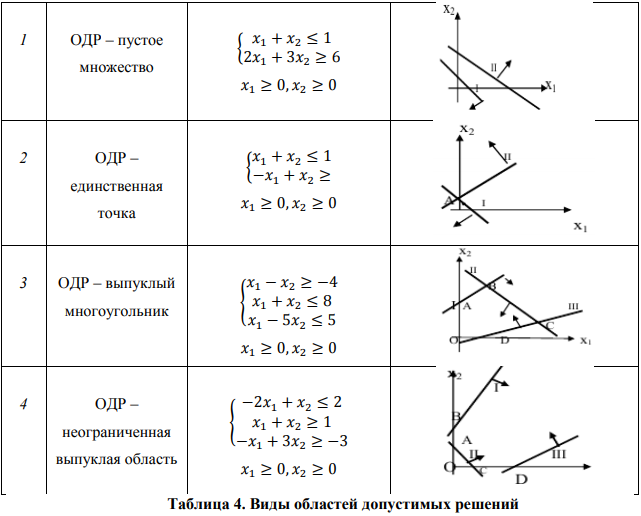
Рассмотренные примеры позволяют сделать вывод о том, что область допустимых решений системы неравенств может быть пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой областью.
Согласно теореме, описанной в предыдущем параграфе, оптимальное решение ЗЛП находится в одной из угловых точек многоугольника допустимых решений. Поэтому решение задачи с ограниченной целевой функцией и не слишком большим числом угловых точек может быть найдено перебором этих угловых точек.
Рассмотрим целевую функцию
Уравнение
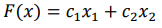
при фиксированном значении 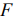 определяет прямую, а при изменении
определяет прямую, а при изменении 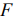 — семейство параллельных прямых с параметром
— семейство параллельных прямых с параметром 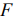 . Вдоль каждой из этих прямых функция цели принимает одно и то же фиксированное значение, поэтому эти линии называют линиями уровня целевой функции [24].
. Вдоль каждой из этих прямых функция цели принимает одно и то же фиксированное значение, поэтому эти линии называют линиями уровня целевой функции [24].
Для решения задачи необходимо среди точек области допустимых решений найти такую точку (точки), в которой целевая функция принимает максимальное значение.
Для этого построим вектор-градиент 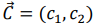 , компонентами которого являются коэффициенты при неизвестных целевой функции, и линию уровня целевой функции, которая имеет уравнение
, компонентами которого являются коэффициенты при неизвестных целевой функции, и линию уровня целевой функции, которая имеет уравнение 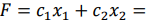
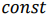 и обладает тем свойством, что она перпендикулярна вектору
и обладает тем свойством, что она перпендикулярна вектору 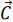 .
.
Линию уровня в направлении вектора 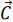 перемещаем до тех пор, пока она не сместится в область недопустимых значений, и все еще будет иметь одну общую точку с ОДР, координаты которой находим из пересечения соответствующих прямых [5].
перемещаем до тех пор, пока она не сместится в область недопустимых значений, и все еще будет иметь одну общую точку с ОДР, координаты которой находим из пересечения соответствующих прямых [5].
Таким образом, можно определить алгоритм геометрического (графического) решения задач линейного программирования:
- Записать уравнения прямых, соответствующих ограничениям, и построить их на плоскости
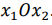 .
. - Определить области, в которых выполняются ограничения задачи.
- Определить область допустимых решений задачи как область пересечения
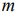 полуплоскостей, соответствующих ограничениям задачи.
полуплоскостей, соответствующих ограничениям задачи. - Определить направление возрастания (убывания) целевой функции
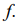
- Определить граничную точку или точки области допустимых решений, в которых целевая функция принимает максимальное (минимальное) значение.
- Определить координаты найденной точки, решая систему уравнений, состоящую из уравнений прямых, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Графический метод решения задачи линейного программирования состоит из двух этапов:
- Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.
- Поиск оптимального решения среди всех точек пространства допустимых решений.
Применение графического метода удобнее рассмотреть на конкретных примерах в двух постановках: для максимума и минимума целевой функции.
Примеры с решением
Пример решения задачи №1:
Задана стандартная математическая модель задачи с двумя неизвестными:
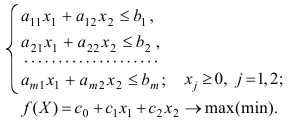
Нахождение решения этой модели на основе ее геометрической интерпретации включает следующие этапы.
- В плоскости
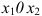 строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств.
строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств. - Находят полуплоскости, определенные каждым неравенством системы.
- Находят выпуклый многоугольник решений всей системы (2.1).
- Строят нормальный вектор целевой функции
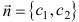 , причем, начало вектора совмещают с началом координат и строят прямую
, причем, начало вектора совмещают с началом координат и строят прямую 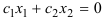 .
. - Передвигают эту прямую в направлении вектора
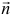 , в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.
, в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений. - Если функция ограничена, то определяют
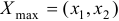 , вычисляют значение функции в этой точке
, вычисляют значение функции в этой точке 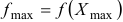 .
.
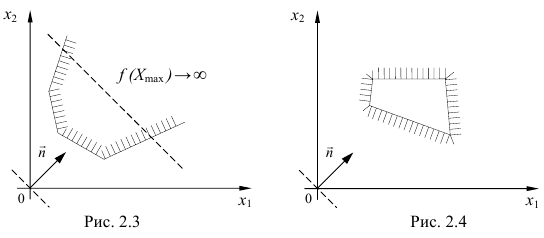
При геометрической интерпретации задач ЛП могут встретиться случаи, изображенные на рис. 2.1. — 2.4.
Рис. 2.1. Задача ЛП имеет единственное решение 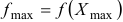 .
.
Рис. 2.2. Задача ЛП имеет бесчисленное множество решений, т.к. целевая функция достигает максимума на отрезке 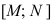 .
.
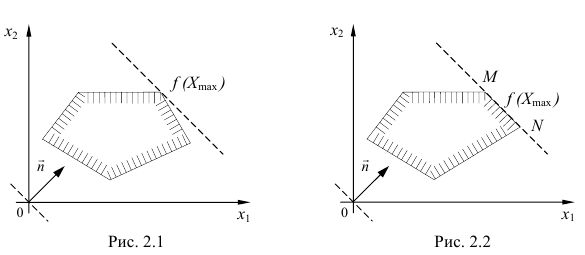
Рис. 2.3. Задача ЛП не имеет решения, т.к. функция неограниченна сверху.
Рис. 2.4. Задача ЛП не имеет решения, т.к. система (2.1) несовместна.
Пример решения задачи №2:
Для производства двух видов изделий 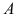 и
и 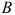 предприятие использует три вида сырья
предприятие использует три вида сырья 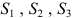 . Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 2.1.
. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 2.1.
Прибыль от реализации одного изделия каждого вида равна 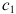 и
и 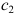 , а общее количество сырья вида
, а общее количество сырья вида 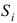 равно
равно 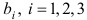 . Считая, что изделия
. Считая, что изделия 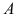 и
и 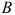 могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной.
могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной.

Решение. Обозначим через 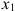 и
и 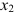 количество изделий первого и второго вида в плане предприятия. Поскольку производство продукции ограничено только сырьем каждого типа
количество изделий первого и второго вида в плане предприятия. Поскольку производство продукции ограничено только сырьем каждого типа 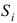 то получим условия:
то получим условия:
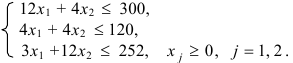
Переменные 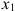 и
и 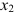 не могут быть отрицательными по смыслу задачи. Вычислим прибыль от реализации продукции и получим:
не могут быть отрицательными по смыслу задачи. Вычислим прибыль от реализации продукции и получим:
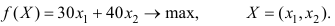
Итак, мы получили стандартную модель с двумя переменными.
Решим задачу линейного программирования геометрически, придерживаясь плана, приведенного ранее.
- Строим прямые
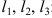 :
:

Обратимся к неравенствам (2.3). Отмстим те полуплоскости, которые им удовлетворяют. Учтем на чертеже и неотрицательность переменных 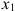 и
и 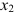 , и получим многоугольник
, и получим многоугольник 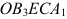 решений данной системы неравенств (см. рис. 2.5).
решений данной системы неравенств (см. рис. 2.5).
- Построим линию уровня — прямую
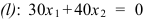 и нормальный вектор
и нормальный вектор 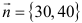 .
. - Передвигая линию уровня
 в направлении вектора
в направлении вектора 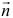 , получим, что в точке
, получим, что в точке  (12, 18) целевая функция будет иметь наибольшее значение. Координаты этой точки находим как координаты точки пересечения прямых
(12, 18) целевая функция будет иметь наибольшее значение. Координаты этой точки находим как координаты точки пересечения прямых 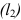 и
и 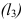 , решая систему уравнений:
, решая систему уравнений:
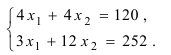
- Запишем окончательный ответ:
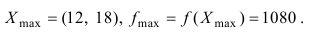
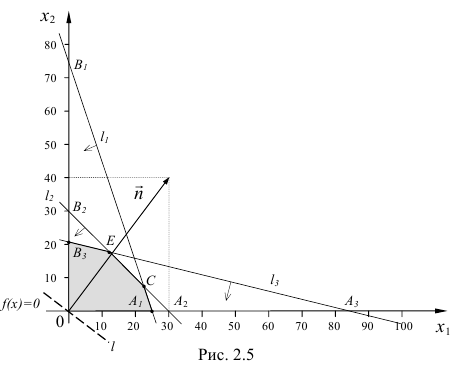
Наибольшая прибыль будет равна 1080 (у.е).
Пример решения задачи №3:
Минимизировать функцию
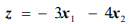
при ограничениях 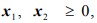
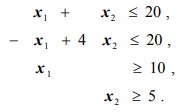
Допустимой областью, изображенной на рис. 1.2, является чегырехугольник 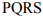 . Два последних ограничения усиливают условия неотрицательности. Функция
. Два последних ограничения усиливают условия неотрицательности. Функция 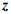 убывает в направлении вектора
убывает в направлении вектора
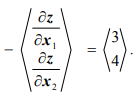
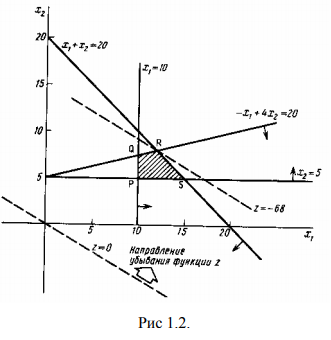
Минимальное значение функции 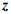 = — 68 и достигается в точке
= — 68 и достигается в точке 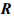 = (12,8). Заметим, что, как и в примере разд. 1.1, минимум достигается в вершине допустимой области. Оптимальным решением задачи является точках
= (12,8). Заметим, что, как и в примере разд. 1.1, минимум достигается в вершине допустимой области. Оптимальным решением задачи является точках 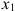 = 2,
= 2, 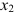 = 8 с минимальным значением функции
= 8 с минимальным значением функции 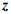 = — 68.
= — 68.
Иногда задача имеет более чем одно оптимальное решение.
Пример решения задачи №4:
Минимизировать функцию
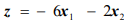
при ограничениях
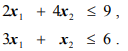
На рис. 1.3 чегырехугольник 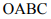 изображает допустимую область
изображает допустимую область 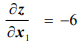 ,
, 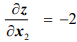 , и, таким образом, вектор
, и, таким образом, вектор 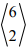 указывает направление убывания функции
указывает направление убывания функции 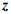 .
.
Любая точка на отрезке 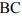 является оптимальным решением. В частности, в вершинах
является оптимальным решением. В частности, в вершинах 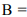
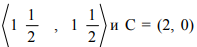 достигаются оптимальные решения, соответствующие одному и тому же минимальному значению функции
достигаются оптимальные решения, соответствующие одному и тому же минимальному значению функции 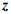 =-12.
=-12.
Любая точка на отрезке 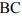 представляется формулой
представляется формулой
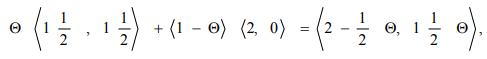
где
Для каждой такой точки значение функции 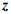 равно
равно
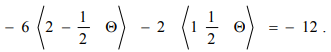
Функция 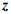 имеет единственное минимальное значение.
имеет единственное минимальное значение.
Иногда решение задачи не ограничено.
Пример решения задачи №5:
Максимизировать функцию
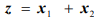
при ограничениях
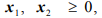
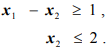
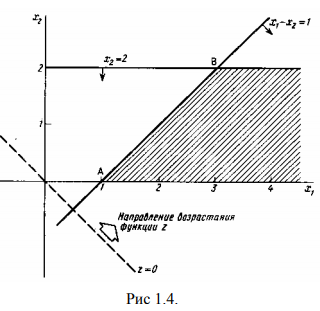
Допустимая область, изображенная на рис. 1.4, не ограничена в направлении, в котором функция 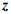 возрастает, т. е. в допустимой области не существует конечной точки, в которой функция
возрастает, т. е. в допустимой области не существует конечной точки, в которой функция 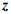 достигала бы максимума. Решение, как и максимальное значение функции
достигала бы максимума. Решение, как и максимальное значение функции 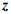 , не ограничено. Однако некоторые задачи с неограниченными допустимыми областями имеют конечные решения. Например, задача максимизации функции
, не ограничено. Однако некоторые задачи с неограниченными допустимыми областями имеют конечные решения. Например, задача максимизации функции 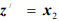 при ограничениях из примера 3 имеет конечное решение.
при ограничениях из примера 3 имеет конечное решение.
Разумеется, если бы задача состояла в минимизации функции 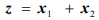 , при тех же ограничениях, то минимум достигался бы в единственной точке
, при тех же ограничениях, то минимум достигался бы в единственной точке 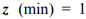 в вершине допустимой области
в вершине допустимой области 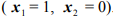 .
.
Иногда задача не имеет решения, поскольку допустимой области не существует.
Пример решения задачи №6:
Минимизировать функцию
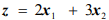
при ограничениях
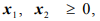
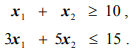
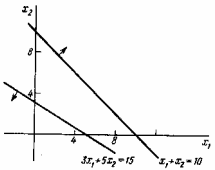
Ограничения задачи противоречивы, поэтому нет допустимых решений (рис. 1.5).
Уже из рассмотренных выше примеров можно вывести несколько характерных черт задач линейного программирования. Во-первых, допустимая область всегда является выпуклым многоугольником, даже в случае, когда она не ограничена. Во-вторых, оптимальное решение всегда достигается в вершинах допустимой области. В примере 2 и вершина  , и вершина
, и вершина  являются оптимальными точками.
являются оптимальными точками.
Эти результаты могут быть обобщены. Сначала покажем, что задачи линейного программирования могут быть приведены к стандартной форме.
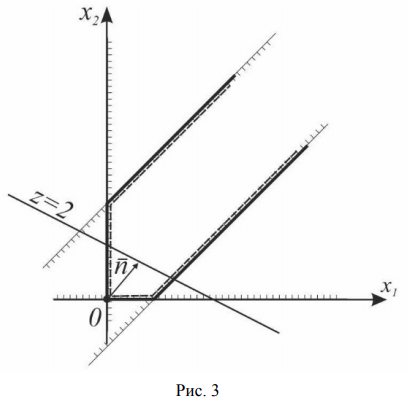
Пример решения задачи №7:
Найти максимум функции 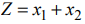 при ограничениях
при ограничениях
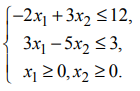
На рис. 3 изображены: неограниченная многогранная область решений данной системы ограничений-неравенств, линия уровня 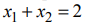 , вектор
, вектор 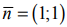 . Функция
. Функция 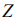 может неограниченно возрастать при заданной системе ограничений, поэтому
может неограниченно возрастать при заданной системе ограничений, поэтому 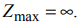 .
.
Пример решения задачи №8:
Найти максимум функции 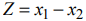 при ограничениях
при ограничениях
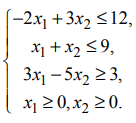
Изображенная на рис. 4 область не содержит ни одной общей точки, которая удовлетворяла бы всем неравенствам системы ограничений, т.е. система ограничений противоречива и не может содержать ни одного решения, в том числе и оптимального.
Пример решения задачи №9:
Найти максимум функции 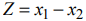 при ограничениях
при ограничениях
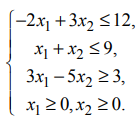
Всем неравенствам системы ограничений удовлетворяют точки треугольника 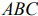 , который и является областью решений (рис. 5). Максимальное значение
, который и является областью решений (рис. 5). Максимальное значение 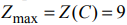 . При построении треугольника
. При построении треугольника 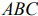 не использовали прямые
не использовали прямые 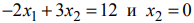 , хотя все точки этого треугольника удовлетворяют неравенствам
, хотя все точки этого треугольника удовлетворяют неравенствам 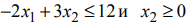 . Таким образом, эти неравенства лишние в системе ограничений.
. Таким образом, эти неравенства лишние в системе ограничений.
Пример решения задачи №10:
Найти минимум функции 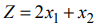 при ограничениях
при ограничениях
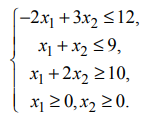
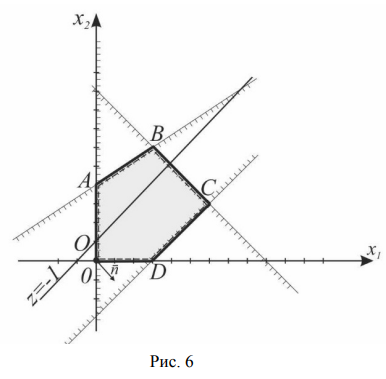
Областью решений данной системы ограничений является треугольник 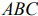 (рис. 7).
(рис. 7).
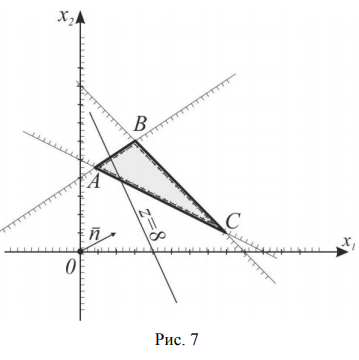
На рис. 7 также изображены исходная линия уровня  и вектор
и вектор 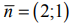 . Так как требуется найти минимум функции, то будем передвигать исходную линию уровня в сторону, противоположную
. Так как требуется найти минимум функции, то будем передвигать исходную линию уровня в сторону, противоположную 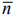 . Минимум функции достигается в угловой точке
. Минимум функции достигается в угловой точке 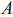 , координаты которой служат решением системы уравнений
, координаты которой служат решением системы уравнений
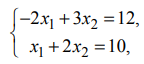
т.е.
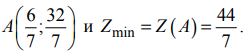
Опорнои прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
На основании приведенных примеров и определения опорной прямой запишем этапы нахождения решения задачи линейного программирования с двумя переменными графическим методом:
- Изображаем область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, то изображаем нормальный вектор
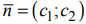 линий уровня и одну из линий уровня, имеющую общие точки с этой областью.
линий уровня и одну из линий уровня, имеющую общие точки с этой областью. - Линию уровня перемещаем до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к максимуму (минимуму) целевой функции, линия уровня уходит в бесконечность, то
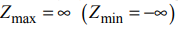 .
. - Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаем систему из уравнений прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорой прямой. Если целевая функция достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.
- Вычисляем значение целевой функции на оптимальном решении.
Графическим методом решаются задачи линейного программирования, записанные в каноническом виде и удовлетворяющие условию 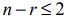 , где
, где 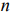 — число неизвестных системы ограничений;
— число неизвестных системы ограничений; 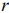 — ранг системы векторов условий. Если уравнения системы ограничений линейно независимы, то ранг
— ранг системы векторов условий. Если уравнения системы ограничений линейно независимы, то ранг 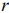 равен числу уравнений системы
равен числу уравнений системы 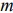 .
.
Возможно эти страницы вам будут полезны:

