Наибольший интерес представляет вопрос о направлении быстрейшего возрастания функции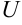 
в точке 
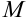. Вопрос просто решается с помощью вектора -градиента функции .
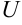Градиентом функции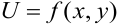 
в данной точке 
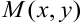называется вектор, расположенный в плоскости 
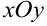с началом в точке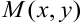
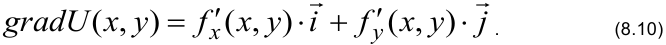
Основное свойство градиента: направление градиента функции в точке является направлением быстрейшего возрастания функции, его модуль равен наибольшей скорости возрастания 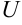в заданной точке.
Другое свойство градиента: он перпендикулярен касательной линии уровня, проходящей через точку начала градиента.
Иллюстрация свойств градиента — на рисунке 8.2. Показаны линии уровня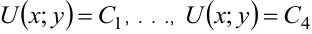 
, причем 
.
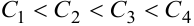Через точку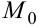 
, лежащую на линии с уровнем 
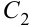проведены касательная и градиент, которые перпендикулярны друг другу. Градиент направлен в сторону возрастания функции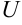 
.
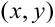8.6 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
Точка 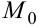называется точкой максимума функции 
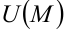, если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки 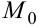. Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
Точки минимума и максимума объединяются под общим названием точки экстремума.
Для функции двух переменных точка 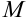имеет две координаты 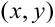для функции трёх переменных — три координаты 
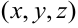. При этом окрестностью точки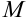 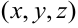является открытый шар с центром в этой точке.
Поиск критических точек, т.е. точек в которых может быть экстремум функции 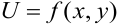, производится при помощи необходимого условия экстремума:
Решение системы (8.12) определяет координаты критических точек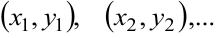 
Однако необходимого условия мало для существования точек экстремума.
Нужно провести исследование критических точек с использованием достаточных условий экстремума.
Для функции двух переменных 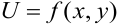введём обозначения для вторых частных производных в критической точке 
:
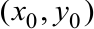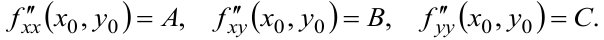
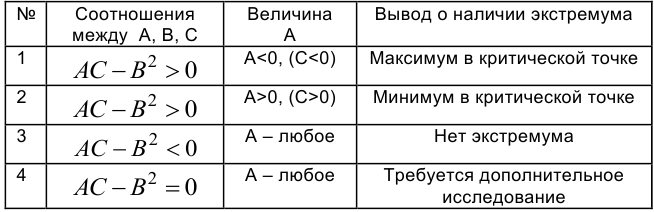
Достаточные условия приводим в таблице 4.
Таблица 4 — Достаточные условия экстремума функции двух переменных
Пример:
Дана функция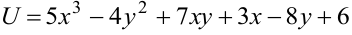 
и точка 
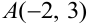. Найти градиент функции 
в заданной точке 
.
Решение:
Используем формулу градиента
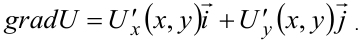
Определяем частные производные и вычисляем их при 
.
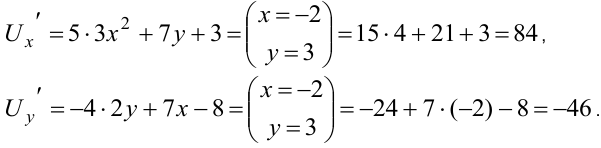
При вычислении частной производной по одной из переменных вторая переменная считается постоянной величиной.
Значения частных производных подставляем в формулу градиента:
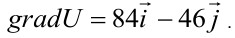
Ответ: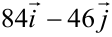 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Полное приращение и полный дифференциал |
| Производная по направлению |
| Экстремум функции двух переменных. Необходимые и достаточные условия экстремума |
| Основные определения о дифференциальных уравнениях |
