Оглавление:


Готфрид Вильгельм Лейбниц. Первая печатная работа по интегральному исчислению
Готфрид Вильгельм Лейбниц. Первая печатная работа по интегральному исчислению. В 1686 году Лейбниц опубликовал мемуары под названием » О глубокой геометрии и анализе.» Неделимый и бесконечный»*«, где символ^впервые обнаружен(на 5) в строчной форме на этот раз. Во-первых, речь идет о теореме Барроу. Если вы обозначаете абсциссу, ординату и денормальность с помощью y, x и p, то ryu = xyh (что можно легко получить, используя бесконечные «характеристические» треугольники, которые содержат подножие yy и yh). «Если вы преобразуете это разностное (дифференциальное) уравнение в Формулу сложения, то оно будет^ p yy ^ x yh. Но из того, что я изложил В моем касательном методе d ^ x yx; для этого vza.
Лейбниц подчеркивает, что его вычисления позволяют ему выражать «трансцендентальные», то есть неалгебраические линии, такие как циклоида, с помощью уравнений. Людмила Фирмаль
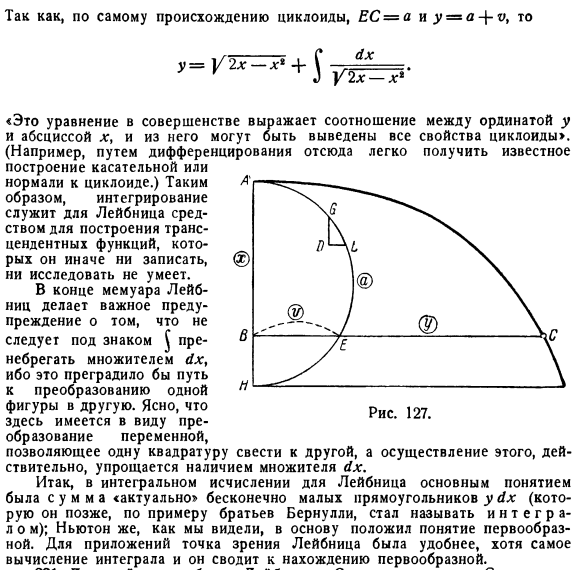
- Наоборот, xyh(потому что есть разница между суммой, или|И чеКак и обычные вычисления, степени, корни, они противоположны. Отсюда ^ p yy = ^ xr, таково содержание теоремы Барроу. Мы упомянем соответствующее место в мемуарах и дополним объяснениями, которые сам Лейбниц дает в своем письме по этому поводу. Рис. 127 показана полуокружности и полукруга дугу циклоиды. Установите радиус окружности равным 1, AB = x%BE = y, BC = y、 Геометрическая теорема Ю= 1-х Г * 1х-х% ух, 01 = г(УГ) Р + {гг) * = Ага. Скорость связи, u2x-ХД> Я. Ага. Скорость связи, u2x -**’ Ае = д ОП = Т,= уу.
- Тогда, согласно хорошо известному q, i = V2x-xi% От начала циклоиды, чтобы быть EC = a и y = a \ V、 = ] / Х2-ХС + с ^ р ^ г Х2-ХС «Это уравнение прекрасно выражает отношение между ординатой y и абсциссой x, что позволяет вывести из него все свойства циклоиды.„(Например, отличая его от этого, можно легко получить хорошо известную структуру касательной или нормали циклоиды. В конце мемуаров Лейбниц дает важное предупреждение, что мы не должны игнорировать фактор 4x под знаком$.
Таким образом, интеграция выступает как средство, с помощью которого Лейбниц конструирует трансцендентальные функции. Людмила Фирмаль
- Здесь понятно, что имеется в виду преобразование переменных. Это позволяет одну квадратуру свести к другой квадратуре, и фактически эта реализация упрощается наличием фактора éx. Так, в интегральном исчислении Лейбница основным понятием была сумма“ действительных » бесконечно малых прямоугольников yx(позже он стал называть ее интегралом для m, следуя примеру братьев Бернулли). как мы видели, Ньютон заложил основу концепции контрдифференцирования. Вычисление интеграла само по себе приводит к нахождению обратной производной, но в случае приложений перспектива Лейбница была более удобной.
Смотрите также:
Решение задач по математическому анализу
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

