Оглавление:








Глава IV
Глава IV 1. В рассматриваемой ситуации нас интересует НЗ ДП через год после последнего платежа. Следовательно, искомая величина x определяется из уравнения x. • «7710,07 = 1000 * Решение с использованием PD.1, x-1000 / 1,07-St7 | 0 07 = 1000 / 1,07-15,7836 = 59, 21. 2.
- В случае уравнения (2.4), где m, N = n, / = 0. 3. Сделайте 1000 = 1, сделайте первый платеж за раз 1. Затем определите максимальный момент n первого платежа первым.
То есть NZ для всех текущих платежей меньше 25. Людмила Фирмаль
Другими словами, определите n из условия «p | o, o8 <25, tg T | o, O8> 25». Однако из PD.1 «74 (0,08 = 24,2149,» t ^ ov = 27,152, и, следовательно, n = 14. Добавление x определяется из условия «7 ^ 1 • 1,08 4-x = -1) 4-й = ( 27.152-1) 4-x = 25. Следовательно, вы должны удалить 1152 из своего аккаунта, потому что x = -1.152.
Также понятно, почему последний платеж был отрицательным. Вы. Фактически, остаток на счете на момент последнего платежа был слишком близок к желаемой сумме: «y ^ = 24,2149. Поэтому интересы следующего года помогли существующим суммам значительно превысить 25: 24 /. 2149-1.08 = 26.152.
- Конечно, такая ситуация не распространена и часто требует положительного дополнительного платежа, хотя в приведенном выше примере подчеркивается, что может произойти ловушка Обратите внимание на заключение, 4 ‘. Пусть № = 2j и 1000 = 1.
Тогда j определяется из уравнения 4-2vja ^ j = 17vJ ° или того же, 1 X 1-X, оs -; — 4-2х -: — = 17×2, x = u5, JJ = 1x-2×2 (1j) 10 (1j) 5-2J-17×2-17 Таким образом, получается желаемое выражение и сечение Вы можете использовать метод последовательной итерации из 4.1,
просто определить начальное значение, зачем принимать то же выражение отмены, но записать его в другой форме: Людмила Фирмаль
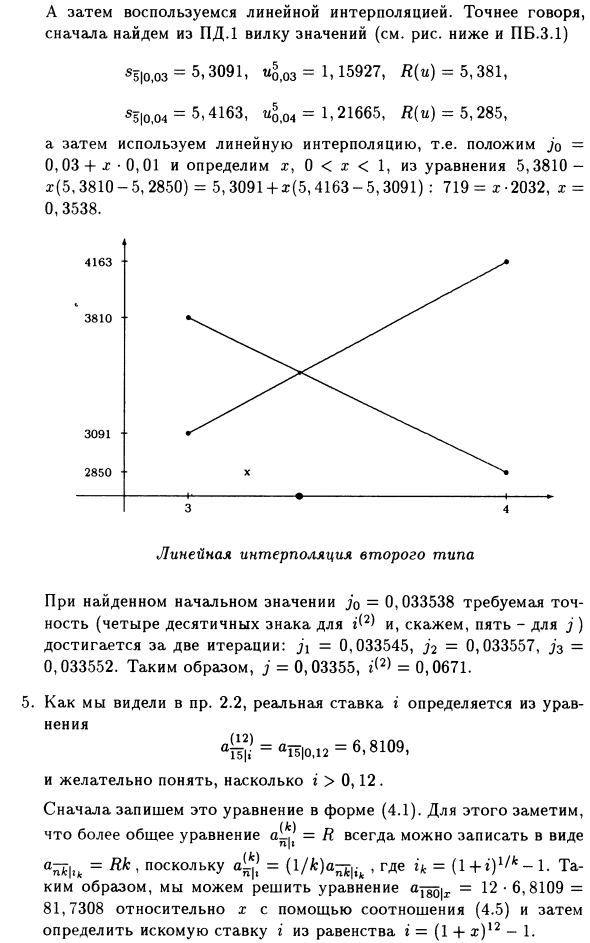
w5s5 | j 255 | j-17> t -e- «51, =« r = K (u). 5 | J 2 4-uJ v Далее используем линейную интерполяцию. Точнее, сначала найдите плагин значения из PD.1 (см. Рисунок ниже и PB.3.1) 55 | o, oz-5.3091, 1 * 0,03 «1> 15927, R (u) -5,381, $ 5 o, O4 = 5,4163, Uq q4 = 1,21665, L (s) = 5,285 и используйте линейную интерполяцию.
Вставьте jo = 0,03 x • 0,01 и определите x, 0 = 0,0671 5. Как мы видели в разделе 2.2, фактическая скорость i определяется по формуле <® = <4510.12 = 6.8109. Желательно понять величину i> 0,12. Это уравнение описывается в виде (4.1).
Обратите внимание, что общее уравнение aL ^ = R всегда можно записать в виде a ^ |. = I *, где a *. * ‘= (L / k) a ^ | ifc, где ik =, Решите уравнение = 12-6.8109 = 81.7308 для х, используя соотношение (4.5) и определите желаемую скорость i из уравнения i = (14- *) 12-1.
Однако здесь желаемая скорость i i больше 0,13, т. е. используйте линейную интерполяцию, чтобы найти только начальное значение g’o, поэтому <12) 15 | 0,13 0,13-6,4624 0, 122842 = 6,8390, все2) = 15 | 0,14 0,14- 6,1422 0,131746 = 6,5270. Ясно, что i> 0,13, линейная интерполяция дает r0 = 0, 1309.
6. Все символы представляют интерес j, 1 L. (1) Точнее, y представляет номер платежа, начиная с оставшегося (последующего) непогашенного остатка. Столица никогда не превышает предписанный уровень L в первый раз.
Но в то же время число p-y представляет количество периодов или платежей, процент которых равен (1), поскольку он рассчитывается по классической формуле (1.4). Поэтому попросите следующий метод решения проблемы: сначала получите другое выражение в Cy, используя доступные рекурсивные отношения в C /, а затем сделайте его эквивалентным первому выражению в (1)
Неравенство, которое выводит выражение для y из x из этого уравнения, а затем определяет простое y. 1) Из уравнений x = yi mi = Ci-iC / и yi = L (ij) jCi-i, C / = [1 (rA- ^] O-1 (1Λ, 1 </ <2 //) C0 = C) где Cy = C (lj) 4 [L (i -;) — x] s5 | J = (C- £) (l; y /, (Li-x) ^. Приравнивая данное значение к выражению в (1), мы получим желаемое выражение * (3) = (С-L) (l;) у L 2)
Как упоминалось выше, у слева от (1) Мы уже заявляли, что это наименьшее целое число, которое удовлетворяет неравенству, но, поскольку мы уже выразили величину x через y, не только записываем неравенство y, но и решаем его, используя известные методы.
Но очень громоздкое неравенство (С-L) (lj) yL iLs5 | j-L 141 из (1) легко и полностью упрощается Простое (5) фактическое, (4) (C-)) (1 + j) va — |, + iLs ^ a -, <(CL ^ a — ^ Lv ^ s ^. 3) В первом приближении величина xQ Возьмите = C / a ^ p и используйте возможность оценить, насколько точно вы погасите кредит при выборе последующего приближения для p во время ЛЛ.
Точнее, используя доступное рекурсивное соотношение Ci = C / _1-xq + iL + -L), если Ci-i> L (т.е. I 0, это означает, что ссуда не была погашена, поэтому вам нужно получить ij> i0. Продолжайте этот процесс, ища вилки и действуя известным образом. 8.
Поскольку C = 3000, L = 1000, n = 12, i = 0,015 и j = 0,01, неравенство (5) для определения числа случаев двойного интереса составляет 2 (/ a) -, = Qn | ~ nV, Q ~ | = a- | + l-un. Следовательно, y6 = 6 (1 − v5) −a ^ + bi5 = b − a ^,. 12. Рассмотрим ситуацию в разделе 2.3, где a (t) = 1, n = 25 и, следовательно, (см. Примечание 2.5) процентная ставка y (t) = 1-0 58. 13.
Значение C (t) должно быть определено двумя способами. С точки зрения раздела 2.3 на основе уравнений (2.16) и (2.19), В предположении, что a (t) = t. В их первом случае нам нужно определить функцию погашения m (t) -кредитов: используя (2.18), уравнение m’-6m = 1 (1)
Как известно, общее решение линейного неоднородного уравнения является суммой общего решения однородного уравнения и конкретного решения неоднородного уравнения и рассчитывается путем изменения константы. Используя эту технику, получаем m (t) = Cu * 4-s- |
Константа C определяется из условия C (n) = 0. Согласно (2.18) m (n) = n, следовательно (см. упражнение 10) m (t) = (nvn-aj) u ‘+ s? | = nvn ~’ -d — p (2) Теперь C (t) = td ^ zy, + (/ D) -, = (/)) -! ‘- (/)); (3) Используйте следующие вспомогательные отношения.
Обратите внимание, что второе уравнение в 3) может быть записано в следующем виде, поэтому его справедливость равна, например, уравнению a ^ T7 | = d’d- | -s? | (См. Упражнение 10 14. Во-первых, докажите эти идентичности, используя интерпретацию: 1. По определению, значение C / представляет собой PP оставшегося платежа для всех nI, но в то же время ,
Этот PP должен быть равен NP самого кредита на данный момент минус любой NP, уже выплаченный 2. C / является первым pl PP, потому что все платежи равны Обратите внимание, что первый член справа — это PP всех n платежей, второй — последний I год, а также в момент времени 0.
На самом деле несложно: 1) Ci = xn E * (E » ‘-E v ) t? = Cu1-e = f + 1 1 1 nn-1 nn 2) C / = z £ u’ — ‘= v’ = x (^ v ‘-E’ ‘) = — «‘ ‘h t = l + l. ‘= 1 1 P- / + 1 15. Пусть C — сумма наследования, а 1000 = 1. Тогда, C = 10aio | o, o35 = 83, 166 и (1.8a) дает сумму процентов за первые пять лет 3,5% -ной ставки как 51 / (0,035) = ω £ (1). — < □; ‘) = 10 (5-gChikhozb) = 11,984. 1
Но сумма процентов, выплачиваемых по ставке i в том же ритме, имеет формулу (где x — сумма постоянного вклада) y («) = r [C» 5 |, —zu4 (Za) ? |] При использовании уравнения (см. Упражнение 14) Ci = Cu1-, поэтому желаемый «дополнительный» процент составляет 0,05 [С $ 5 | ОО5-10uq 05 (/ a) 4 | 005] -t / ( 0,035) = 5737.
Если оплата производится в конце года, (80 ООО / год), аТТ | о, О8-5000 = 8868,78, а9 | 0,09 2) 80 000 (1,09) 9- (80 000 / год ^ унция) * 9 | O, o9-5000 a9 | 0,09 = 10450,58
Смотрите также:
| Глава II. | Глава V. |
| Глава III. | Глава VI. |

