Оглавление:


Геометрический смысл условия дифференцируемости функции двух переменных.
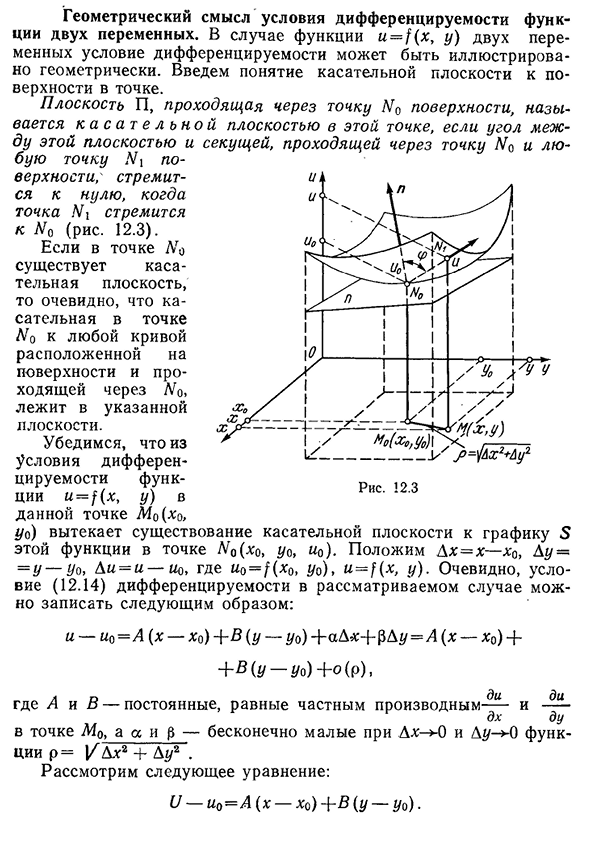
- Геометрический смысл условия Дифференцируемости функции двух переменных. Для функции u=f(x,y)двух переменных условие Дифференцируемости может быть геометрически проиллюстрировано. В поверхность вводится понятие контактной плоскости в определенной точке. Поверхность N, проходящей через точку поверхности нет,этот Дю-эта поверхность и называется К а в плоскости Л Л Л Н О й плоскости секущая, точки бую Н поверхность\;
пункт 12.3). Если в точке нет касательной плоскости, то ясно, что касательная в этой точке N находится на поверхности, а на любой кривой, проходящей через o, лежит на указанной плоскости. Условие Дифференцируемости функции u=f (x, y) в заданной точке Afo (o>Yo) означает наличие касательной плоскости к графу
S этой функции в точке No(xo, y o, A0) D x-x-Ho,=U-UO,Di=I-I0, где Uo=f(o, y0), u f=(x,y, y). Людмила Фирмаль
Очевидно, что Дифференцируемость vie (12.14) в рассматриваемом случае равна I-I0=A (x-Ho) 4 — ®(u-Uo) 4-ADH-| — RDU=A(x-Ho) 4-+b (U-Uo)+o (p)> Если угол между проходящей точкой, — через точку N q и Liu- Все требования мы можем- «N B-константа, равная производной в частных производных di— — — и DX В точках Mo, a и p-tion p=V DH2+DU2. Рассмотрим следующее уравнение: U-I0=A(x—x0)+B (u-Uo). DH Didu
Infiniti — > — 0 и Du — > — 0 funk-474CH. 12. Функции некоторых переменных Уравнение проходит через точку No (xo, y o, I0) в декартовой системе координат (x, y, U), и определение плоскости N с нормальным вектором n={L, B, -1*совпадает с определением аналитической геометрии.} * N o R m a l n s m V e K t o R O M поверхность-это любой ненулевой вектор N, перпендикулярный этой поверхности. . Докажите, что эта плоскость N является касательной плоскостью в точке Y
- грани 3. Для этого достаточно сделать следующее: 1)плоскость N проходит через точку плоскости S, 2) угол f между нормалью n этой плоскости и любым секущим NfN t, Утверждение 1) плоскость S очевидна. Перейдем к доказательству утверждения 2). Вычислите косинус угла f, используя известную формулу для Косинуса углов между двумя векторами. Поскольку координаты вектора p равны a, B—1,а координаты вектора n0ni секущие-x-x0,y-yo и-I0(см. Рисунок). 12.3),
то cos f= ^(-U-x0)+V (|/- u0)—(I-IO)_ / D2+B2+]/(x_Zo) 2+(1 / / / o) 2+(u_U ()) 2 • От дифференциации состояния функции u=f(Х, У), {х-хо)АГ Б (г-г О)—(я-значения i0)=о(п). Поток, Таким образом,|cos f|<т. е. lim f= -. Два. I o (R) 1=I o (R)i U (x— » o) 2+(1/ — Uo)2P Утверждение 2) доказано. О, когда p — ^0, Таким образом, Дифференцируемость функции u=f (x, y) в точке M0 (XO, yo) с геометрической точки зрения равна Дифференцируемости касательной плоскости к графу функции
u=f (x, y) в точке N0 (x0, yo, IO). Поскольку коэффициенты A и B являются Людмила Фирмаль
частными производными, вычисленными с помощью Af0 (x0,Yo), соответственно, уравнение касательной плоскости можно записать в виде Нормальный вектор n=/—,—, — 1 касательная плоскость- I. DH du J STI называется n o r M al u относительно поверхности u=f(x, y) в точках N0 (x0, yo, z0).
Смотрите также:
| Частные производные функции нескольких переменных | Всюду плотные и совершенные множества |
| Дифференцируемость функции нескольких переменных | Достаточные условия дифференцируемости |

