Генеральная совокупность и выборка с примерами решения и образцами выполнения

Приступим к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.

Пусть требуется изучить множество однородных объектов (это множество называют статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить соответствие детали стандартам, а количественным — контролируемый размер детали.

Лучше всего осуществить сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, их недоступность и т. п. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, проводя сплошное обследование, мы должны будем уничтожить всю партию.

Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.

Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.

Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.

Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 —объем генеральной совокупности, а 10 —объем выборки.

Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна

Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет взята с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.

Статистическое распределение выборки. Полигон. Гистограмма

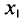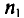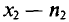Пусть из генеральной совокупности извлечена выборка, причем , наблюдалось раз, раз, 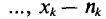раз и 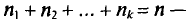объем выборки. Наблюдаемые значения 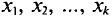называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений 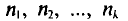называют частотами, а их отношения к объему выборки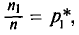 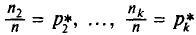— относительными частотами. Отметим, что сумма относительных частот равна единице:

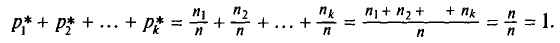
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.

Пример:

Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:

Найдем относительные частоты:

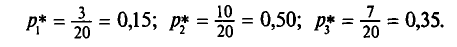
Поэтому получаем следующее распределение:

Для графического изображения статистического распределения используются полигоны и гистограммы.

Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант 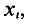на оси Оу— значения частот 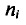(относительных частот ).

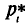Пример:

Рис. 14 представляет собой полигон следующего распределения:

Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала 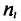— сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотам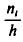и (или 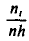, где n —объем выборки). Площадь i-го частичного прямоугольника равна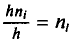

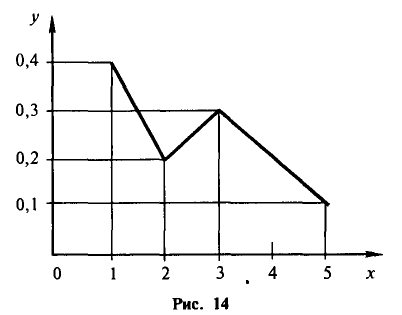
(или 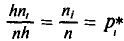). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).

Пример:

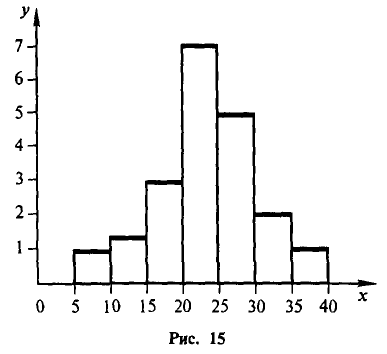
Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:

Оценки параметров генеральной совокупности по ее выборке

Выборка как набор случайных величин

Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X—как случайную величину, а х —как одно из возможных значений X.

Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного определения) параметров, которыми описывается это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака 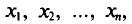полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.

Опытные значения признака X можно рассматривать и как значения разных случайных величин 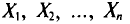с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит, 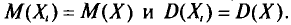Величины 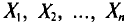можно считать независимыми в силу независимости наблюдений. Значения 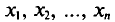в этом случае называются реализациями случайных величин 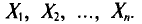Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — это значит найти функцию от наблюдаемых случайных величин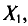 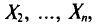которая и дает приближенное значение оцениваемого параметра.

Генеральная и выборочная средние. Методы их расчета

Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.

Определение:

Генеральной средней 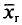(или а) называется среднее арифметическое значений признака генеральной совокупности.

Если все значения 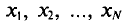признака генеральной совокупности объема N различны, то

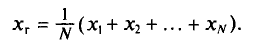
Если же значения признака 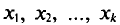имеют соответственно частоты 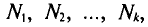причем то

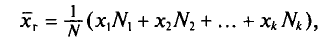
или

Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.

Пусть все значения 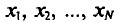различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то

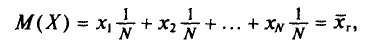
т. е.

Такой же итог следует, если значения 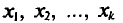имеют соответственно частоты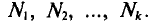

В случае непрерывного распределения признака X по определению полагают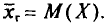

Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.

Определение:

Выборочной средней 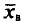, называется среднее арифметическое значений признака выборочной совокупности.

Если все значения 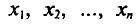признака выборки объема n различны, то

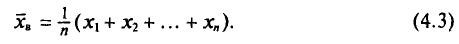
Если же значения признака 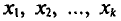имеют соответственно частоты 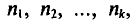причем , то

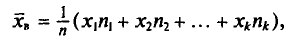
или

Пример:

Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю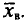

Согласно формуле (4.4), имеем:

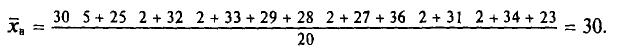
Итак,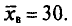

Далее, не уменьшая общности рассуждений, будем считать значения 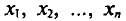признака различными.

Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины 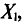а их среднее арифметическое

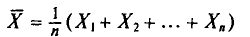
есть тоже случайная величина.

Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины 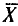, которая называется выборочной средней случайной величиной.

Найдем 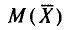, пользуясь тем, что 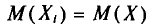(см. п. 1).

С учетом свойств математического ожидания (см. гл. II) получаем:

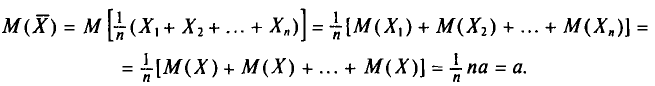
Итак, 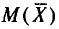(математическое ожидание выборочной средней) совпадает с а (генеральной средней).

Теперь найдем 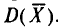Так как 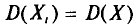(п. 1) и 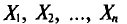независимы, то, согласно свойствам дисперсии (см. гл. II), получаем

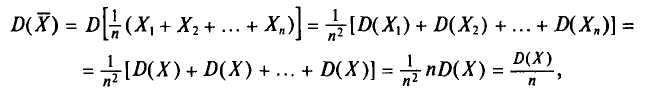
T. e.

Наконец, отметим, что если варианты 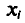—большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.

Так как

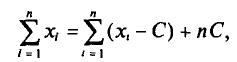
то формулу (4.3) можно преобразовать к виду

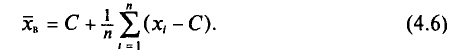
За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n).

Пример:

Имеется выборка:

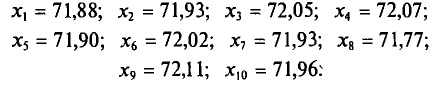
Требуется найти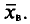

Возьмем С =72,00 и вычислим разности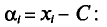

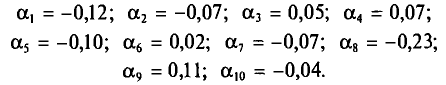
Их сумма: 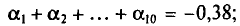их среднее арифметическое 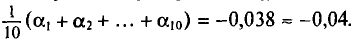Выборочная средняя

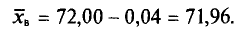
Генеральная и выборочная дисперсии

Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.

Определение:

Генеральной дисперсией D, называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней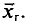

Если все значения 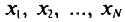признака генеральной совокупности объема N различны, то

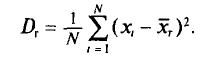
Если же значения признака 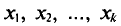имеют соответственно
частоты 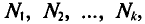причем то

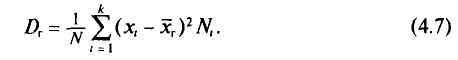
Пример:

Генеральная совокупность задана таблицей распределения:

Найдем генеральную дисперсию.

Согласно формулам (4.1) и (4.7), имеем:

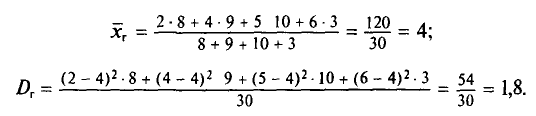
Генеральным средним квадратическим отклонением (стандартом) называется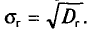

Пусть все значения 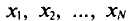различны.

Найдем дисперсию признака X, рассматриваемого как случайная величина:

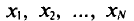
Так как 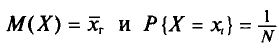(см. п. 2), то

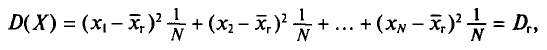
т. е.

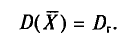
Таким образом, дисперсия D(X) равна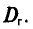

Такой же итог можно получить, если значения 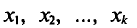имеют соотвественно частоты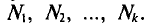

В случае непрерывного распределения признака X по определению полагают

С учетом формулы (4.8) формула (4.5) (п. 2) перепишется в виде

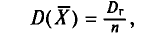
откуда 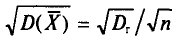или 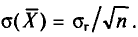Величина 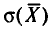называется средней квадратической ошибкой.

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 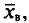вводят выборочную дисперсию.

Определение:

Выборочной дисперсией 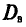, называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней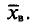

Если все значения 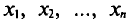признака выборки объема n различны, то

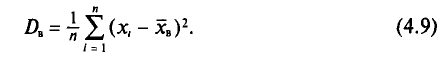
Если же значения признака 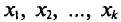имеют соответственно частоты 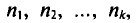причем 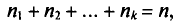то

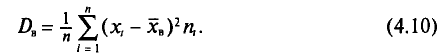
Пример:

Пусть выборочная совокупность задана таблицей распределения:

Найдем выборочную дисперсию. Согласно формулам (4.4) и (4.10), имеем:

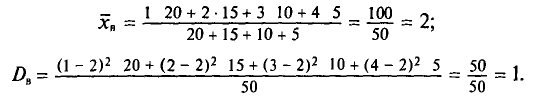
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:

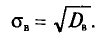
В условиях примера 2 получаем, что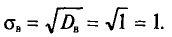

Далее, не уменьшая общности рассуждений, будем считать значения 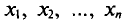признака различными.

Выборочную дисперсию, рассматриваемую нами как случайная величина, будем обозначать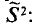

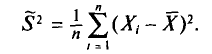
Теорема:

Математическое ожидание выборочной дисперсии равно 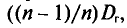т.е.

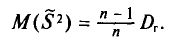
Доказательство:

С учетом свойств математического ожидания (см. гл. II) получаем

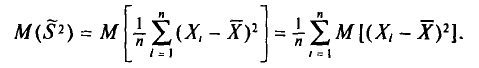
Вычислим одно слагаемое 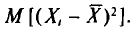Имеем

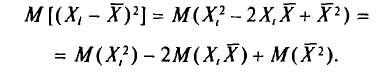
Вычислим по отдельности эти математические ожидания.

Согласно свойству I дисперсии (см. гл. И) и формулам (4.2), (4.8) имеем

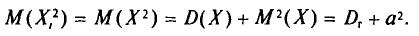
Далее, с учетом свойства 4 математического ожидания (см. гл. II)

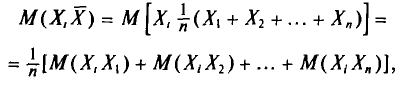
но слагаемое этой суммы, у которого второй индекс равен і, т.е. 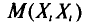, равно 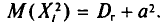У всех остальных слагаемых 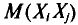индексы разные. Поэтому в силу независимости 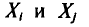(см. гл. II)

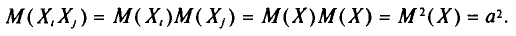
Так как имеется n-1 таких слагаемых, то

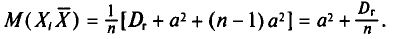
В силу свойства 1 дисперсии (см. гл. П) получаем

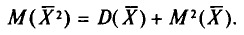
Нами уже найден (см. пп. 2 и 3):

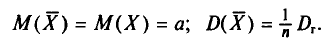
Поэтому

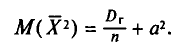
Таким образом,

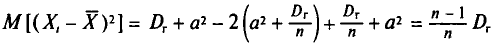
и не зависит от индекса суммирования і. Поэтому

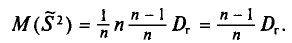
Что и требовалось доказать.

В заключение этого пункта отметим, что если варианты 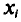— большие числа, то для облегчения вычисления выборочной дисперсии 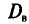, формулу (4.9) преобразуют к следующему виду:

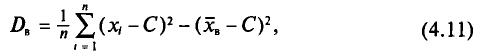
где С—ложный нуль.

Действительно, с учетом формулы (4.3) имеем

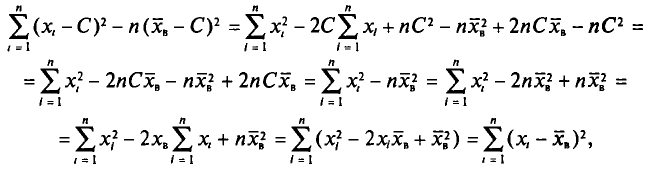
откуда

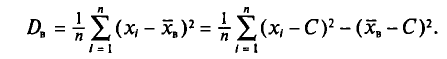
Пример:

Для выборки, указанной в примере 2 из п. 2, найдем 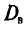(ложный нуль остается прежним С= 72,00)

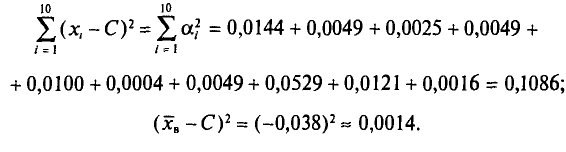
Наконец, согласно формуле (4.11)

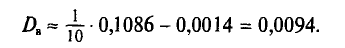
Оценки параметров распределения

Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 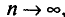где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например, 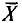(см. п. 2) является оценкой генеральной средней, а 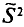(см. п. 3) — оценкой генеральной дисперсии 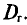Обозначим через 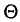оцениваемый параметр, через 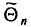— оценку этого параметра 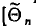является выражением^ составленным из 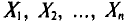(см. п. 1)]. Для того чтобы оценка 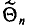давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.

Несмещенной называют оценку 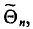математическое ожидание которой равно оцениваемому параметру 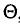, т. е. 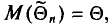в противном случае оценка называется смещенной.

Пример:

Оценка 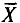является несмещенной оценкой генеральной средней а, так как 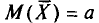(см. п. 2).

Пример:

Оценка 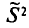является смещенной оценкой генеральной дисперсии 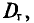так как, согласно установленной выше теореме (см. п. 3),

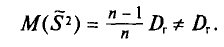
Пример:

Наряду с выборочной дисперсией 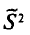рассматривают еще так называемую исправленную дисперсию 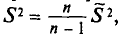которая является также оценкой генеральной дисперсии. Для 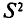с учетом установленной выше теоремы (см. п. 3) имеем

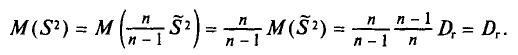
Таким образом, оценка 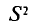в отличие от оценки 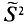является несмещенной оценкой генеральной дисперсии. Явное выражение для 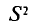имеет вид

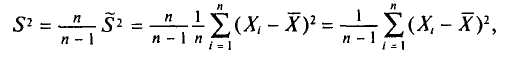
T. e.

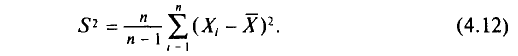
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.

Состоятельной называют такую оценку 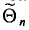параметра 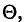, что для любого наперед заданного числа 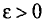вероятность 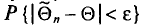при 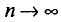стремится к единице*. Это значит, что при достаточно больших n можно с вероятностью, близкой к единице, т. е. почти наверное, утверждать, что оценка 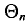отличается от оцениваемого параметра 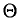меньше, чем на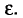

Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.

Заметим, что несмещенная оценка 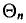будет состоятельной, если при 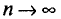дисперсия стремится к нулю: 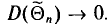Это следует из неравенства Чебышева ((2.33) см. § 2.8, п. 1).

Пример:

Как было установлено (см. п. 3), 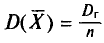. Отсюда следует, что несмещенная оценка 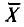является и состоятельной, так как

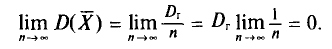
Можно показать, что несмещенная оценка 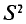является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки 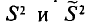отличаются множителем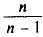, который стремится к 1 при 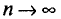. На практике 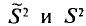не различают при n > 30.

Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:

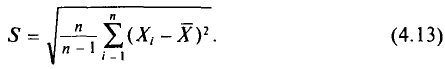
Левые части формул (4.12), (4.13), в которых случайные величины 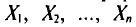заменены их реализациями 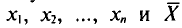выборочной средней 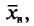будем обозначать соответственно через 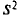и s

Отметим, что если варианты 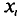— большие числа, то для облегчения вычисления 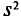формулу для 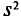аналогично формуле (4.9) преобразуют к виду

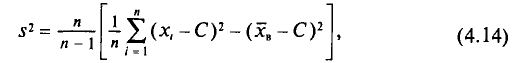
где С—ложный нуль.

Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.

Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.

Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.

Пример:

С плодового дерева случайным образом отобрано 10 плодов. Их массы 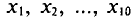(в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления 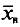и s пo формулам (4.6) и (4.14) введем ложный нуль С=250 и все необходимые при этом вычисления сведем в указанную таблицу:

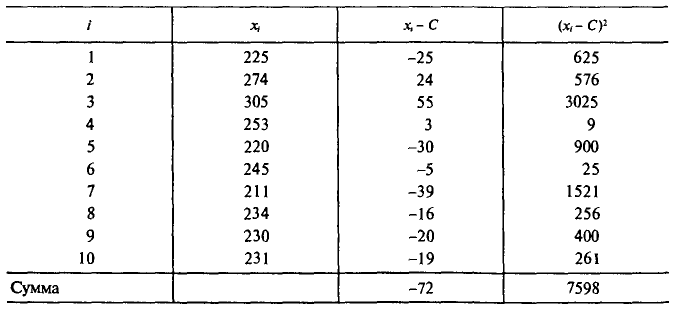
Следовательно,

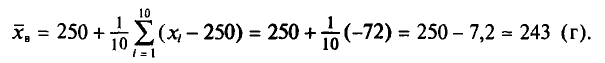
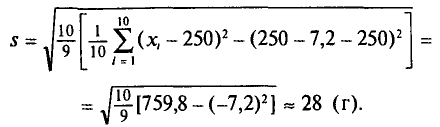
Отсюда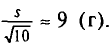

Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.

Оценка генерального среднего квадратического отклонения массы плода равна 28 г.

Пример:

Через каждый час измерялось напряжение в электросети. Результаты измерений (в вольтах) представлены в следующей таблице:

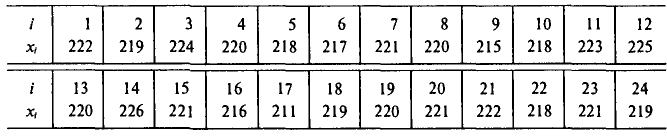
Найти оценки для математического ожидания и дисперсии результатов измерений. Оценки для математического ожидания и дисперсии найдем по формулам (6) и (14), положив С=220. Все необходимые вычисления приведены в нижеследующей таблице:

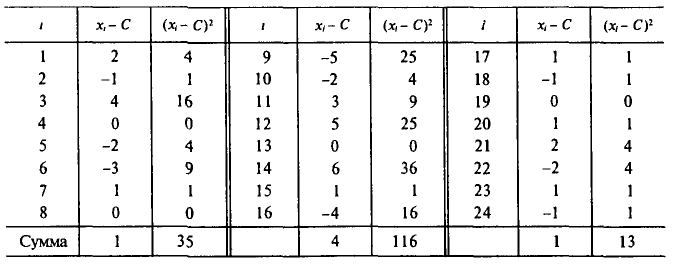
Следовательно,

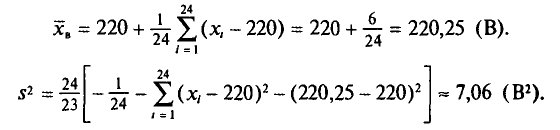
Доверительные интервалы для параметров нормального распределения

Пусть — оцениваемый параметр, 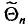— его оценка, составленная из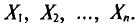

Если известно, что оценка 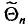является несмещенной и состоятельной, то по данным выборки вычисляют значение 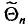и считают его приближением истинного значения 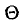. При этом среднее квадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными. Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало.

Если же о распределении имеется какая-либо информация, то можно сделать больше.

Здесь речь будет идти об оценке параметров а и 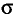случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.

Пусть 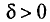— некоторое число. Если выполняется неравенство 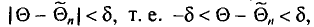что можно записать в виде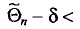 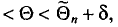то говорят, что интервал 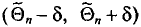покрывает параметр 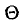. Однако невозможно указать оценку 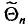такую, чтобы событие 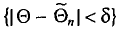было достоверным, поэтому мы будем говорить о вероятности этого события. Число 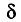называется точностью оценки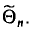

Определение:

Надежностью (доверительной вероятностью) оценки 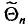параметра 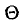0 для заданного 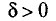называется вероятность 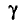того, что интервал 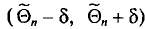покроет параметр 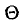, т. е.

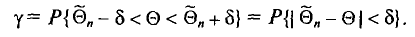
Заметим, что после того, как по данным выборки вычислена оценка 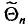, событие 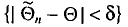становится или достоверным, или невозможным, так как интервал 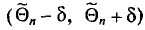или покрывает 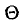, или нет. Но дело в том, что параметр 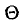нам неизвестен. Поэтому мы называем надежностью 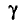уже вычисленной оценки 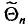вероятность того, что интервал 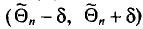, найденный для произвольной выборки, покроет 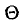. Если мы сделаем много выборок объема n и для каждой из них построим интервал 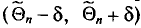, то доля тех выборок, чьи интервалы покроют 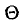, равна .

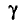Иными словами, 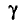есть мера нашего доверия вычисленной оценке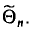
Ясно, что, чем меньше число 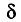, тем меньше надежность .

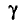Определение:

Доверительным интервалом называется найденный по данным выборки интервал 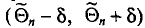, который покрывает параметр 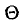с заданной надежностью .

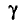Надежность 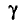обычно принимают равной 0,95 или 0,99, или 0,999.

Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр 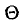. Но в этом можно быть уверенным на 95% при 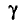= 0,95, на 99% при 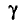=0,99 и т. д. Это значит, что если сделать много выборок, то для 95% из них (если, например, 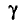= 0,95) вычисленные доверительные интервалы действительно покроют .

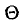Доверительный интервал для математического ожидания при известном

Доверительный интервал для математического ожидания при известном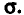

В некоторых случаях среднее квадратическое отклонение о ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях.

Итак, пусть случайная величина X распределена нормально с параметрами а и 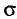, причем 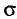известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью 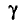. Данные выборки есть реализации случайных величин 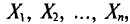имеющих нормальное распределение с параметрами а и 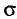(§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина 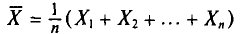тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3)

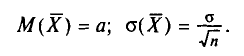
Потребуем, чтобы выполнялось соотношени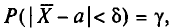е где 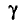—заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим

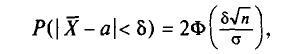
или

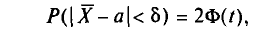
где

Найдя из равенства (4.15) 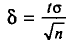можем написать

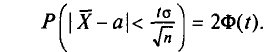
Так как Р задана и равна 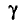, то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на ):

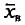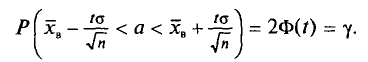
Смысл полученного соотношения таков: с надежностью у можно утверждать, что доверительный интервал 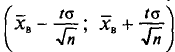покрывает неизвестный параметр а; точность оценки 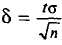. Здесь число t определяется из равенства 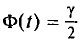(оно следует из 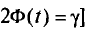по таблице приложения 3.

Как уже упоминалось, надежность 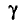обычно принимают равной или 0,95 или 0,99, или 0,999.

Пример:

Признак X распределен в генеральной совокупности нормально с известным 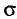= 0,40. Найдем по данным выборки доверительный интервал для а с надежностью 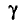= 0,99, если n = 20, 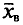= 6,34.

Для 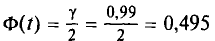находим по таблице приложения 3
t=2,58. Следовательно, 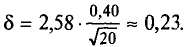. Границы доверительного интервала 6,34 — 0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99.

Доверительный интервал для математического ожидания при неизвестном

Доверительный интервал для математического ожидания при неизвестном .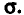

Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и 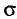. Оказывается, что случайная величина (ее возможные значения будем обозначать через t)

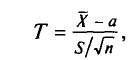
где n —объем выборки; 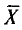— выборочная средняя; S—исправленное среднее квадратическое отклонение, имеет распределение, не зависящее от а и 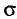. Оно называется распределением Стьюдента*.

Плотность вероятности распределения Стьюдента дается формулой

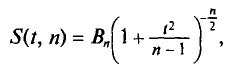
где коэффициент 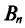зависит от объема выборки.

Потребуем, чтобы выполнялось соотношение

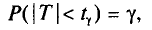
где 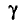—заданная надежность.

Так как S(t, n) — четная функция от t, то, пользуясь формулой
(2.15) (см. § 2.5), получим

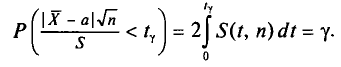
Отсюда

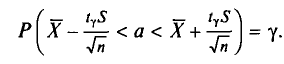
Следовательно, приходим к утверждению: с надежностью 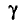можно утверждать, что доверительный интервал 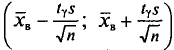покрывает неизвестный параметр а, точность оценки 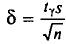-. Здесь случайные величины 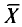и S заменены неслучайными величинами 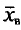и s, найденными по выборке.

В приложении 4 приведена таблица значений 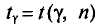для различных значений n и обычно задаваемых значений надежности.

Заметим, что при 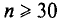распределение Стьюдента практически не отличается от нормированного нормального распределения
(см. § 2.7, п. 2). Это связано с тем, что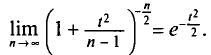

Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 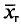с надежностью 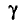=0,99, если 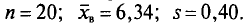Для надежности 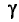=0,99 и n = 20 находим по таблице приложения 4 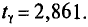Следовательно, 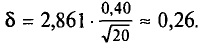. Концы доверительного интервала 6,34-0,26 =
= 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает 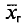с надежностью 0,99.

Доверительный интервал для среднего квадратического отклонения

Для нахождения доверительного интервала для среднего квадратического отклонения 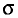будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3).

С надежностью 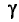можно утверждать, что доверительный интервал 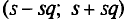покрывает неизвестный параметр 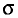; точность оценки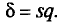

В приложении 5 приведена таблица значений 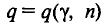для различных значений n и обычно задаваемых значений надежности .

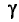Пример:

Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 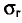с надежностью 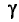=0,95, если n = 20, s = 0,40.

Для надежности 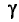=0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40 0,37 = 0,15. Границы доверительного интервала 0,40-0,15 = 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает 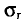с надежностью 0,95.

Пример:

На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратическое отклонение — 20 кг.

Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратического отклонения с той же надежностью.

При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.

Решение:

1) Согласно условиям задачи, 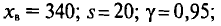n = 20.

Пользуясь распределением Стьюдента, для надежности у=0,95 и n = 20 находим в таблице приложения 4 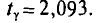Следовательно, 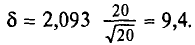Границы доверительного интервала 340-9,4 =
= 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95.

Можно считать, что в данном случае истинная масса измерена 9 4 достаточно точно (отклонение порядка ).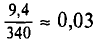

2) Для надежности у =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 20 * 0,37 = 7,4. Границы доверительного интервала 20 — 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 < 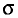< 27,4, откуда можно заключить, что 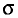определено неудовлетворительно (отклонение порядка 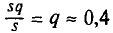— почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n.

Примечание. Выше предполагалось, что q<1. Если q> 1, то, учитывая, что 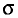>0, получаем 0<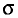<s + sq. Значения q и в этом случае определяются по таблице приложения 5.

Пример:

Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найдем доверительный интервал для 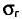с надежностью 0,999.

Для надежности у = 0,999 и n= 10 по таблице приложения 5 находим q=1,80.

Следовательно, искомый доверительный интервал таков’

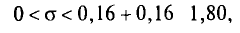
или

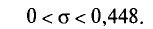
Оценка истинного значения измеряемой величины

Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 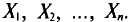Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 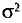(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно 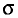неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.

Пример:

По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 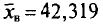и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью у = 0,99.

Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном 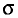) при помощи доверительного интервала

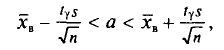
покрывающего а с заданной надежностью у=0,99.

Пользуясь таблицей приложения 4 по у=0,99 и n = 9, находим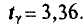

Найдем точность оценки:

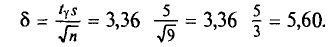
Границы доверительного интервала

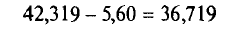
и

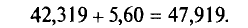
Итак, с надежностью у=0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719<а< 47,919.

Оценка точности измерений

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения 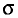случайных ошибок измерений. Для оценки 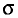используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то утверждение, приведенное в п. 4, применимо для оценки точности измерений.

Пример:

По 16 независимым равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s=0,4. Найдем точность измерений с надежностью у = 0,99.

Как отмечено выше, точность измерений характеризуется средним квадратическим отклонением о случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала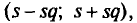 покрывающего 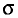с заданной надежностью у=0,99 (см. п. 4). По таблице приложения 5 по у = 0,99 и n=16 найдем q = 0,70. Следовательно, искомый доверительный интервал таков:

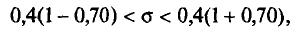
или

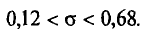
Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Нормальный закон распределения
15. Определение законов распределения случайных величин на основе опытных данных
16. Системы случайных величин
17. Нормальный закон распределения для системы случайных величин
18. Вероятностное пространство
19. Классическое определение вероятности
20. Геометрическая вероятность
21. Условная вероятность
22. Схема Бернулли
23. Многомерные случайные величины
24. Предельные теоремы теории вероятностей
25. Оценки неизвестных параметров