Формулы прямоугольников

Попытаемся заменить криволинейную трапецию ступенчатой фигурой, состоящей из прямоугольников. Для этого выполним следующие действия (рис. 47.2).

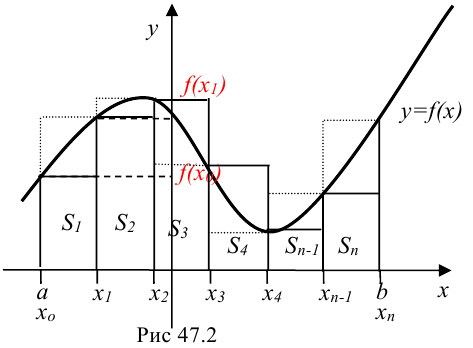
1. С помощью точек разобьём отрезок на равных частей. Тогда длина каждого отрезка будет равна 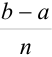. Её называют шагом разбиения и обозначают .

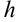2. На каждом отрезке 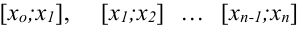построим прямоугольники высотой .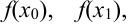

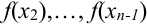3. Найдем площадь каждого прямоугольника как произведение его длины на ширину:

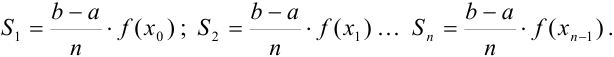
Тогда сумма площадей всех прямоугольников 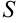будет равна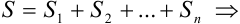

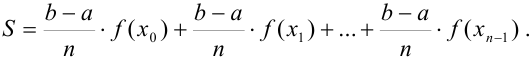
Вынесем 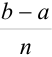за скобки: .

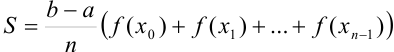Поскольку сумма площадей всех прямоугольников 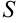приближенно равна площади криволинейной трапеции, то можно считать, что

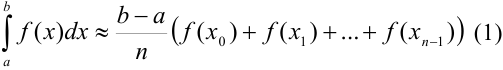— формула прямоугольников.

Если в качестве высоты прямоугольников брать значения функции не в левом, а в правом конце отрезка (рис. 47.2), то формула прямоугольников будет иметь вид:

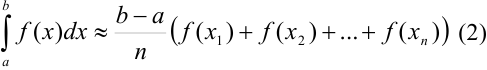— формула прямоугольников.

Пример №47.1.

Вычислите определенный интеграл :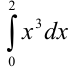

а) по формуле Ньютона-Лейбница;

б) по формулам прямоугольников (число точек деления ).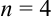

Решение:

а) 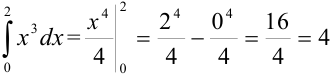— точное значение .

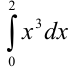б) Выпишем подынтегральную функцию 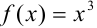и рассмотрим ее на отрезке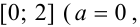 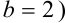. Поскольку число точек деления отрезка равно 4, найдем ширину каждого отрезка (шаг) по формуле .

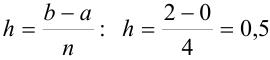Для удобства вычислений все расчеты будем выполнять в электронных таблицах Microsoft Excel. В качестве шапки таблицы можно предложить следующий вариант:

В столбце будет указываться номер выполняемого шага: .

В столбце 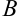будут располагаться значения 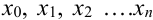. Поскольку 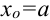, то в ячейку занесем значение 0. Чтобы найти значение 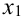, которое будет находиться в ячейке 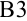, достаточно к началу промежутка прибавить ширину шага . В ячейке 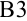будет находиться число 0 + 0,5 = 0,5. Для нахождения каждого последующего значения 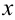к предыдущему необходимо прибавлять ширину шага до тех пор, пока 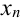не будет равно .

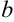В столбце 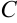будут содержаться значения функции в точках 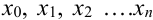, необходимые для расчета значения определенного интеграла по формулам (1) и (2). Чтобы их получить достаточно ввести формулу в ячейку 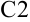. В нашем примере она будет иметь вид: 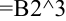. Для заполнения столбца оставшихся значений 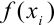можно воспользоваться возможностями автозаполнения. Тогда таблица будет иметь вид:

Рассчитаем приближенное значение определенного интеграла по формуле прямоугольников (1) в ячейке 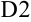, по формуле прямоугольников (2) в ячейке 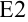. Множитель 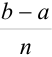нами уже вычислен, он равен 0,5, поэтому формулы в ячейках 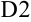и 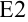будут иметь вид:

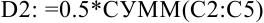(поскольку суммируются значения функции, начиная с и заканчивая ;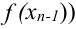

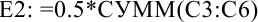(суммируются значения функции, начиная с 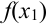заканчивая ).

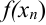Результирующая таблица будет следующей:

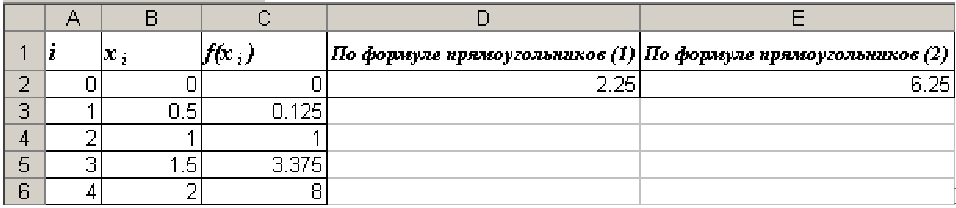
Видим, что полученные по формулам прямоугольников значения определённого интеграла (2,25 и 6,25) достаточно сильно отличаются от его реального значения (4). Очевидно, что с увеличением числа точек деления приближенное значение определенного интеграла будет ближе к реальному. Но все равно метод прямоугольников относится к числу наименее точных. Рассмотрим другие методы численного интегрирования.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Метод касательных.

Задача численного интегрирования.

Формула трапеций.

Формула парабол (Симпсона).