Если заменить график функции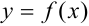 
не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точною формулу вычисления интеграла 
.
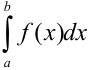Для использования метода Симпсона число точек деления должно быть четным. Тогда представим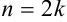 
. Приведем формулу парабол без вывода:
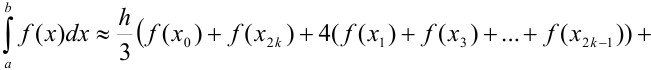
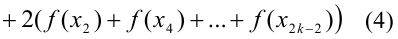
— формула парабол (Симпсона), где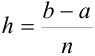 
ширина шага.
Рассмотрим применение данного метода на конкретном примере.
Пример №47.3.
Вычислите приближенное значение определенного интеграла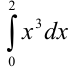 
по формуле парабол (число точек деления 
).
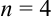Решение:
Воспользуемся решением примера 47.1. Рассмотрим функцию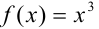 
на отрезке 
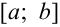, который разбит на четыре части шириной 
.
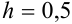В уже созданной в Microsoft Excel таблице в ячейку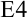 
запишем формулу для расчета приближенного значения определенного интеграла 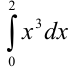по формуле парабол (4).
Перед скобкой должен стоять множитель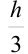 
. В нашем случае он будет равен 
.
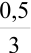Выражение в скобках представляет собой сумму
- первого и последнего значения функции,
- умноженную на 4 сумму значений функций, имеющих нечетный индекс
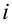, - умноженную на 2 сумму значений функций, имеющих четный индекс 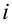(за исключением
).
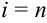Тогда формула в ячейке 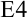будет иметь вид: 
.
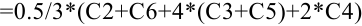Расчетная таблица будет следующей:
Видим, что приближенное значение определенного интеграла, вычисленное по формуле парабол (4) в данном примере совпадает с точным значением, вычисленным по формуле Ньютона-Лейбница. Из трех рассмотренных нами формул формула парабол дает лучшее приближение определенного интеграла 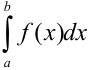, чем формулы прямоугольников и трапеций.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Формулы прямоугольников. |
| Формула трапеций. |
| Задача численного решения дифференциальных уравнений. |
| Метод Эйлера. |
