Оглавление:




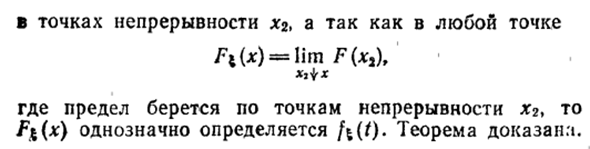

Формулы обращения для характеристических функций
- Формула обращения характеристической функции В §37 было установлено, что каждой функции распределения Fi (x) соответствует характеристическая функция / $ (/). Предположим, что существует непрерывная плотность Pb (x). Далее рассчитывается характеристическая функция По формуле о /; (>) = J eitxPi (x) dx, (22) -Объектно-ориентированный.
- То есть f (f) — преобразование Фурье функции ЦЦχ) \ о Выражение интеграла ^ \ fi (i) \ dt — О Обращение преобразования Фурье (22): OO = $ e ~ l, Xh (t) dt (23) — О Основываясь на этой формуле, мы докажем формулу обращения общего случая. Сначала докажем некоторые вспомогательные утверждения.
Пусть лемма 2.ξ и m] независимы. Людмила Фирмаль
Если ξ имеет функцию распределения F (x) и m] равномерно распределены в интервале [a, b], существует плотность P \ + r \ (*), представленная следующим уравнением , Pl + C W e-a- ‘ Доказательство. По составу формулы оо б W *) = J Fl (x-y) Pri (y) dy = T ± j \ F (x-y) dy = — О ха ~ T ^ a \ F & dZ- <24> XB <24) на основе любого X \ p (dc — //) — p (dg) ^ T -Объектно-ориентированный и lpa (-v) -p (*) l 0. Тогда вы можете выбрать δ> 0 так, чтобы при \ y \ выполнялось неравенство \ p (x-y) -sg e / 2.
Поскольку плотность р (х) имеет предел, существует постоянная С <оо, поэтому (25) 1 £ / K4 0 |> Выберите 0 и P || r \ l ^ -jj;} <затем Все | 9 |> 0 ° имеют неравенство | pe () — p (x) \ + /) — FX (* — /) = lim-I? е ~, х> ч (0 дт. o- * 0 31 J 1 — О (26) Доказательство. Пусть r — случайная величина. £ независима, £ — функция распределения F \ (x) tr], равномерно распределенная по интервалу (-1,1), а £ имеет нормальное распределение с параметрами (0,1).
- Тогда по лемме 2 ξ + 1r \ имеет плотность. Ftix + D-F ^ x-l) p [x) = -2 / — ‘ £ ++ имеет отличительные черты h (D ^ -e-— el ,, Поэтому его плотность pn (x) выражается формулой обращения (23). оо, р W — E $ <27> фильтрат Лемма 3 v, Fl (x + 1) -Fl (x-l) хм /? „(*) = — * — Rj-i — (28) о- * 0 Если x + / и x — / переместиться к границе смежной точки F% (x) \ (27) и использовать уравнение (28), излучаем (2G).
Теорема 2. Существует только одна функция распределения, соответствующая каждой характеристической функции f% (t). Ого) Доказательство. В уравнении (26) разность F \ (X) между точками jc2 = a * + / и jcj = Jkr- / непрерывности F ^ (x) определяется однозначно из / * (/). Предположим, что Fi (xg) однозначно определяется из непрерывной точки xb разности fh (* 3) -Fi (x () X \ — * — °°). Теорема доказана.
В точке непрерывности х2, в любой точке Fi (x) -lim FixJ, Xj + x Здесь, если ограничение применяется к точкам с непрерывностью x2, ft (x) однозначно определяется fi (t). Людмила Фирмаль
Смотрите также:
Решение задач по математической статистике
| Ветвящиеся процессы | Определение математического ожидания |
| Определение и простейшие свойства характеристических функций | Формулы для вычисления математического ожидания |
Если вам потребуется помощь по математической статистике вы всегда можете написать мне в whatsapp.

