Формулы для скорости и расхода при истечении из отверстий и насадков

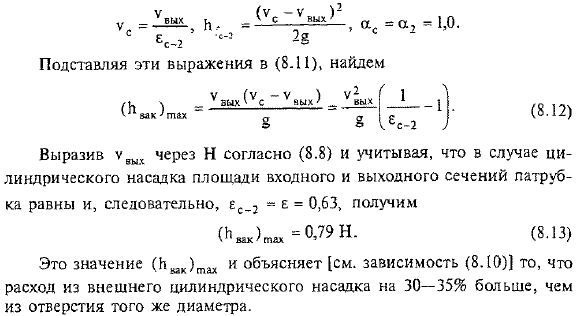
Формулы для скорости и расхода при истечении из отверстий и насадков

Формулы для скорости и расхода при истечении из отверстий и насадков. При постоянном уровне воды в резервуаре учитывают отток жидкости в атмосферу из вертикальной стенки отверстия (рис. 8.3). для определения расхода жидкости используют уравнение Бернулли по схеме, описанной в разделе 2. 6.2. 1. Обеспечивает обзор 1-1 и 2 разделов s-S. 2.Плоскость сравнения 0-0 рисуется через центроид сечения 4.В этой формуле 2,= ч; п= ПК = Р3; г;= 0; 2С = 0; далее 3.Уравнение Бернулли может быть выражено как a = ac = 1.0; US-неизвестное значение. Ю. Г. [ы = ^> т {_с хорошо ~~ Коэффициент потери давления при сжатии струи (по экспериментальным данным^ _s = 0,06). 5.Результаты, полученные с помощью уравнения Бернулли (8.1), после простого преобразования、 Где F0-коэффициент скорости отверстия.

Экспериментальное исследование и теоретическое решение задачи истечения из скважины на основе модели скрытого течения невязкой жидкости. Людмила Фирмаль

• Найти расход по формуле 3 =(8-4） Вы должны знать площадь секции сжатия gc. Обычно через площадь отверстия выражаются следующим образом: Яш = ССО(8.5） Где е-степень сжатия струи. (см. Главу 14) показало, что величина е в случае полного сжатия изменяется в пределах Малого предела, поэтому ее трудно рассчитать на практике. Подставляя (8.2) и (8.5) в (8.4), получаем формулу течения вида Где p0™E (p0 = 0,61-коэффициент холловского разряда. Аналогичное рассуждение выполняем в случае разлива из внешнего цилиндрического сопла (сопла Вентури).

В качестве расчетной площади поперечного сечения для записи уравнения Бернулли можно выбрать выходную площадь поперечного сечения трубы, где свободная поверхность и давление воды в баке считаются равными атмосферному давлению(см. рис.8.2). в результате использования уравнения Бернулли по приведенной выше схеме получаем формулу для скорости выходного сечения сопла. Где ™ CBx-коэффициент потери давления на входе в трубопровод (т. е. он сжимает поток в сечении c — c и расширяется до размера, определяемого поперечным сечением трубы).Эксперимент показывает^ ax = 0.5). fn-коэффициент скорости сопла; fn = 0,82.

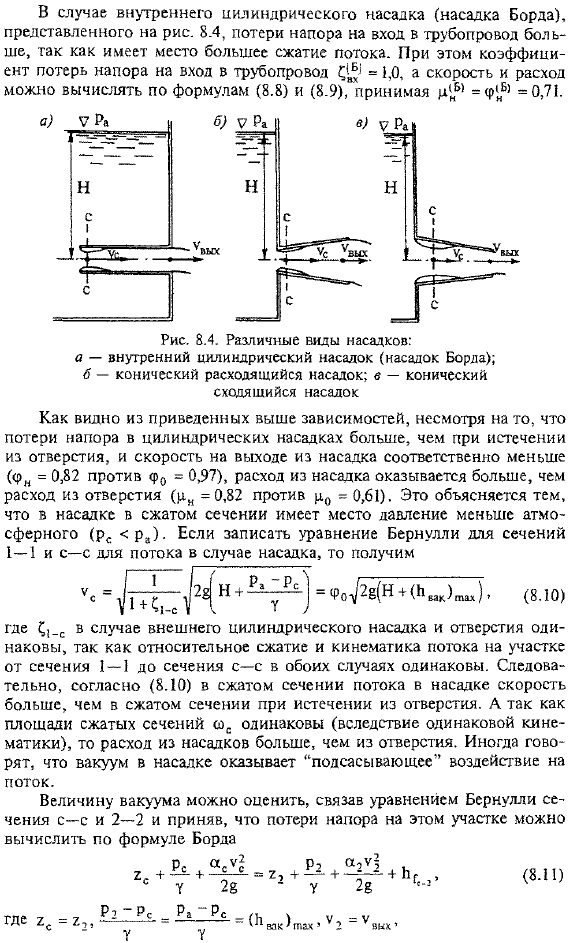
• Форма формулы подачи сопла. Для внутреннего цилиндрического сопла (шарового сопла), показанного на Рис. 1 8.4, потеря давления на входе в трубопровод велика. Это связано с тем, что происходит сжатие потока increases. In в этом случае коэффициент потерь давления на входе в трубопровод= 1,0, а скорость и расход могут быть рассчитаны по формулам(8.8) и(8.9), причем c nB! с (фб) −0.71. Как видно из приведенных зависимостей, потери давления цилиндрического сопла больше, чем при сливе из отверстия, и скорость на выходе из сопла соответственно меньше (fn = 0,82 против φ0= 0,97), но поток из сопла больше, чем поток из отверстия(pk = 0,82 против t0 = 0,61)

Если вы запишете уравнения Бернулли в разделах 1-1 и c—c о потоке в случае сопла, вы можете увидеть: Здесь относительное сжатие и кинематика потока в сечениях от сечения 1-1 до сечения c—c одинаковы в обоих случаях, поэтому^ _c в случае внешних цилиндрических сопел и отверстий является same. So, согласно (8.10), скорость сжатой части потока в сопле больше скорости сжатой части, когда она вытекает из отверстия. А так как площадь сжатого участка gc одинакова (согласно той же кинематике), то расход из сопла будет больше, чем расход из сопла. hole.

.Это связано с тем, что давление сопла в компрессионной секции меньше атмосферного. Людмила Фирмаль

• It иногда говорят, что вакуум в сопле оказывает «всасывающее» влияние на поток. Где: 7 = 2、 Размер вакуума можно оценить, соединив секции c-c и 2-2 с уравнением Бернулли и предположив, что потери давления в этой секции можно рассчитать по формуле платы. В соответствии с (8.8) uayh выражается в H, а в случае цилиндрических сопел, принимая во внимание, что площади входного сечения сопла и выходного сечения равны, получают таким образом ec, 2-E = 0,63. Подставляя эти выражения в (8-11)、 Это значение (b^) ^также объясняет [опорная зависимость (8.10)), что расход из внешнего цилиндрического сопла на 30-35% больше, чем расход из отверстия того же диаметра.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Постеленное закрытое задвижки.
2. Истечение из отверстий и насадков. Основные понятая.
3. Истечение через нецилиндрические насадки.
4. Истечение через отверстия и насадки «под уровень».