Формула Валлиса

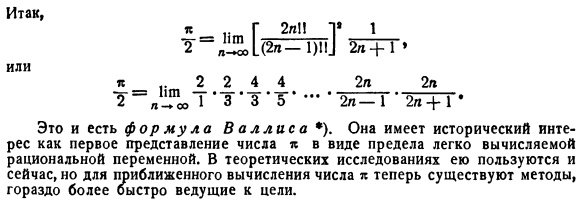
Формула Валлиса

Формула Валлиса. Из Формулы (5) легко вывести знаменитую формулу Уоллиса, опубликованную в 1655 году его бесконечным количеством арифметики. Предполагая 0* -^ -, существует неравенство $ 1Pvy + 1 x $ W8ya x $ t8L_1.

Это произведение сходится крайне медленно, поэтому для практического вычисления числа π формула Валлиса мало пригодна. Людмила Фирмаль

• Закрепите эти неравенства в диапазоне от 0 до 0 К т. Я К т. Пять К Т. 81P * L + 1 X 4.X 1 5 SHGL X 1×1 8 / 1-1 X ax. О, о, о, о. Поэтому, благодаря (5)、 Г \ (2л-1)!! tf(2 ″ −2) м (2л + 1) 1! ^ 2l II ’ 2(2l −1) 11 * Или Г 2л! 1 1 * 1 ТФ 2л! ]] 8 1 | (2l-1) и] 2l + 1 2 / _(2l-1)!/ ] ’2Н.

• Из 2 крайних выражений различия 1 г 2lI 1 * ^ 1 ТФ (2л + 1) 2л [(2л—) \ \ 2-я * 2 ’ для η -°°, очевидно, существует тенденция к нулю, и это является общим ограничением. заметим, что ym переходит в f подстановкой x -Λ. Или Так… * D 2lI 1 * Один 2л + 1 * * 2 2 4 4 2l 2l Т ^ Л ^ Т ^ Т \ Т \ Т \ З-* 2У ^ Т \ » 21 + Т Это уравнение для Уоллиса*).

Исторически формула Валлиса имела значение как один из первых примеров бесконечных произведений. Людмила Фирмаль

• Оно имеет исторический интерес как первое представление чисел, так и как предел рациональных переменных, которые легко calculated. In теоретические исследования его сейчас используют, но для приближенного вычисления числа k существует гораздо более быстрый метод.

Смотрите также:

Решение задач по математическому анализу

Формула замены переменной в определенном интеграле.	Формула трапеций.
Интегрирование по частям в определенном интеграле.	Параболическая формула.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.