Формула трапеций

Формула трапеций

Формула трапеций. Предположим, нам нужен конкретный расчет Является интегралом х/(x) х. Где/(x) это Но… Жуткая [a, b] непрерывная функция. В § 3 я в основном использовал формулу (A)для вычисления аналогичного интеграла с использованием антипроизводных. Однако конечная форма антипроизводной выражается только для функций узкого класса. Внешне, как правило, приходится прибегать к различным приблизительным методам расчета. Эти методы обеспечивают приближенное выражение для интеграла через значение подынтегрального выражения, вычисленного для нескольких значений независимого variable.

В простейшем случае получение такого выражения облегчается геометрическими соображениями, поскольку некоторый Интеграл может быть интерпретирован как область «криволинейной трапеции». Людмила Фирмаль

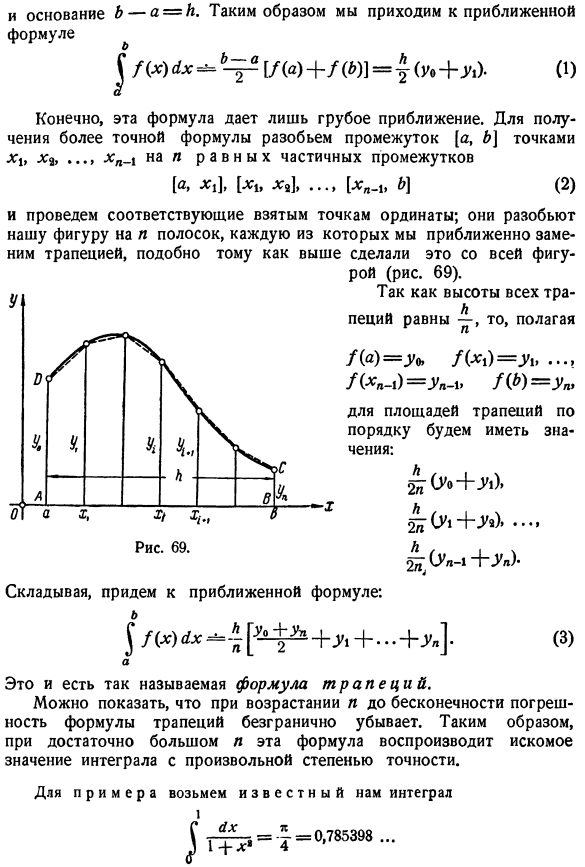
• Кривая y = f (x), ограниченная[N°17b], сводит задачу к ABC (рис.68) и приближенному расчету таких областей. Прежде всего, естественно заменить кривую CO хордой, а криволинейную трапецию обычной one. To определите площадь последней, достаточно знать только первую и последнюю вертикальные координаты. /(а)= уа, ХБ） * )Формула указана в оригинале. н А основание b-a = K. Следовательно, это будет приближенная формула. / / () ЛК + л -= ^ [/(А)+ /(6)] = а(V,+> -). (1） [а,.],[ХВ.], б \ Мне.»••• (2） Рисует соответствующую ординату к полученному point. As мы сделали со всей фигурой выше, фигура разделена на полосы, каждая из которых почти заменена трапецией. В 0 га Я Стадо (рис. 69). С высоты всех тигров М Л Песий равен и положен /（2）= ^ 0、/（Х1)= У1,… /(Хп-1)= уя-1> /(б)= уя、 Для трапециевидной области, получены следующие значения.

• Конечно, эта формула показывает только грубое approximation. In для того чтобы получить более точную формулу, можно задать интервал[a, b \до точки xi X * …разделите bynnn_1 и разделите его на подинтервалы, равные η. Кроме того, приближенная формула достигнута. (3） Но… Это так называемый трапециевидный тип. Поскольку я расту до бесконечности, это показывает, что ошибка формулы трапеции уменьшается бесконечно. Поэтому для достаточно большой самости эта формула воспроизводит целевое значение интеграла с произвольной точностью. Затем примените к нему расчетную приближенную формулу, возьмите i = 10 и вычислите 4 знака.

Чтобы формула действительно подходила для приближенных расчетов, нужна удобная формула для ошибок. Людмила Фирмаль

• По трапециевидной формуле、 АГ1 = 0.1 мм = 0.9901 ДГ * = 0.2 ул = 0.9615 Х9-0.3-Анг = 0.9174 Д:4 = 0.4 У4 = 0.8621 DG5 = 0.5 у9 = 0.8000 Х9 = 0.6 у9-0.7353 Х7-0.7 ^ 7 = 0.6711 ХВ = 0.8 Ыб = 0.6098 Х9 = 0.9 у9-0.5525 Сумма 1.5000 7.09981 = 0.78498×0-0.0 У0 = 1.0000 * г = В0 У10-0.5000 Сумма 7.0998 Полученный приблизительный результат отличается от истинного значения лишь менее чем на 0,0005. Конечно, читатель понимал, что ошибка здесь может быть оценена именно потому, что он заранее знал точное значение integral. In Это позволяет не только оценить погрешность с определенной самооценкой, но и выбрать ту самооценку, которая обеспечивает требуемую точность. вернитесь к этому вопросу в n * 191.

Смотрите также:

Решение задач по математическому анализу

Интегрирование по частям в определенном интеграле.	Параболическая формула.
Формула Валлиса.	Дополнительные члены приближенных формул.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.