Оглавление:



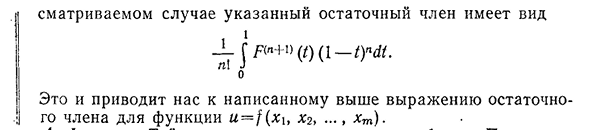

Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме
- Уравнение Тейлора в Лагранжевой форме и с остаточным членом в интегральной форме. Условимся обозначить производную / GTH функции t переменной u=f (xi, x2, — XT) в точках M символами dku\M и space1. Докажем следующие важные теоремы. Пусть A12: 15 N>0-целое
число, функция и — = f (xi, x2)……. XT), точка Mo (xi, x2,…, HT) и P+1X дифференцируемы в указанной окрестности. Тогда приращение суммы этой функции: Au=f(M)-f (M0)! В точке M она может быть представлена в следующем виде:&u=du+ — d2u+… М0 2! /
M0 — dnu4 — — — — — -!—- dn+1u|>n\m»(n+1)! В этом случае N-это, в общем случае, L4 (x y x2, Людмила Фирмаль
… Он входит в Формулу dku \ Ma и равен DX<= — Xi-XP. Формула (12.50) называется f o R M ulo y T Y e l o R a из-за функции u=f (M), а точка Mo-z l o e n I I, и конечный член формулы (12.50) n a zy VA et SIA полный рабочий день. Д О К а з а т е л ь с Т В О. для уменьшения записи выведем две переменные x и y функции n= / (x, y). N+1 точка
производная от t0. Напомним, что формула Tay-498CH. 12. Функции некоторых переменных Лора, имеющая центр разложения для функции u=F(t) переменной, имеет следующий вид:F (t)=F(t0)+F'(t0)F(2>(t0) (t-t0Y+… •• * + — V F w&) V-W+dn+1u\w(t-tj~4~+^Y~G~}+I|L'(«+0dx. < / 04-OADH du ) А в Формуле (12.55) — из соотношения dx и dy:(12.54) в L=A/=1-0=1. Таким образом, формула (12.55) dx-d t\x=\x и dy=d t\y=\y.
- (12.56)»подставим dku\t, dn+1u|1-е?- /- +(x a-x°2)- y -+… +(x,p—x°t)y — ] \ k\DHG DH2DHT*=1 X f(XP x2,. ** HT)4-(Hg X1) — и(Xg^2″ » N. • — (I+1)! ДХ! DHG, e h d / » 4-1g. Report , * * * +(x>n-x t) — f(X1+ ДИГИДРОТЕСТОСТЕРОН ] 4-6(Х1-х?), x°+0(x2-x°),… H°t+6 (HT-HT)(12.57>S l e d s t V I e. функция u = f (xi, x2,…, HT) выполняет то же условие, что и теорема 12.15, причем все частные производные этой функции непрерывны в
рассматриваемой е окрестности точки МО, остаточного члена., То есть последние члены формулы (12.50) и (12.57) могут быть описаны следующим образом О Л?=l J x f(x°+t (Xg-X°), X°+1(x2-X°)……… Xm+t (xm-x°m)) dt. Эта форма остаточного члена естественно называется подынтегральной функцией. Для того чтобы получить выражение Тейлора с остаточным членом интегральной формы,
умножим остаточный член выражения Тейлора на функцию одной переменной Людмила Фирмаль
F (t), которая учитывается при доказательстве теоремы 12.15 RAS-300CH. 12. Функции некоторых переменных Если возможно, оставшийся член принимает вид-G. F («+i») (?) (1-т)НДТ. n\J Ноль. Это связано с тем, что функции u=f (xi, x2,…, ХТ).
Смотрите также:
| Производная логарифмической функции | Другая запись формулы Тейлора |
| Дифференциалы высших порядков | Формула Тейлора с остаточным членом в форме Пеано. |

