Формула Ньютона — Лейбница является основной формулой интегрального исчисления.
Важность формулы в том, что она даёт простой способ вычисления определённого интеграла, который позволяет не прибегать к вычислению предела интегральных сумм 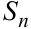 .
.
Формула Ньютона — Лейбница:
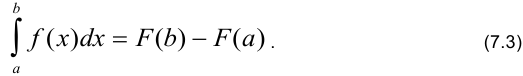
Здесь функция 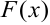 — первообразная для подынтегральной функции
— первообразная для подынтегральной функции 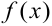 . Формула (7.3) показывает, что определённый интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.
. Формула (7.3) показывает, что определённый интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.
Применение формулы Ньютона — Лейбница покажем на примере.
Пример:
Вычислить интеграл
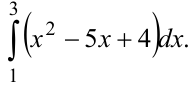
Решение:
Для вычисления интеграла находим первообразную и вычисляем её приращение на отрезке интегрирования. Используем свойства определённого интеграла №1, №2.
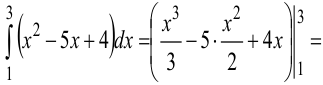 (найдена первообразная подынтегральной функции; пределы интегрирования проставлены после вертикальной черты) =
(найдена первообразная подынтегральной функции; пределы интегрирования проставлены после вертикальной черты) =
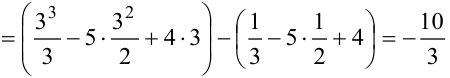 (вычислена разность между значениями первообразной при
(вычислена разность между значениями первообразной при 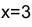 и
и 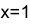 ).
).
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

