Рассмотрим функцию 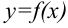 , непрерывную на отрезке
, непрерывную на отрезке 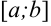 . Пусть
. Пусть 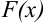 — какая либо первообразная
— какая либо первообразная  на отрезке
на отрезке 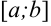 . Тогда имеет место формула, получившая название формула Ньютона-Лейбница:
. Тогда имеет место формула, получившая название формула Ньютона-Лейбница: 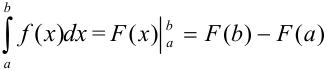 .
.
Формула Ньютона-Лейбница даёт удобный способ вычисления определенного интеграла.
Чтобы вычислить определенный интеграл от непрерывной на отрезке 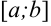 функции, нужно:
функции, нужно:
- Найти неопределенный интеграл от функции
 , выбрав
, выбрав 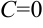 . Справа поставить вертикальную черту, рядом с которой указать верхнюю и нижнюю границы интегрирования.
. Справа поставить вертикальную черту, рядом с которой указать верхнюю и нижнюю границы интегрирования. - В полученное выражение вместо
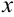 следует подставить сначала верхнюю границу
следует подставить сначала верхнюю границу 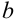 , поставить знак «минус», подставить в выражение вместо
, поставить знак «минус», подставить в выражение вместо 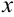 нижнюю границу
нижнюю границу 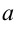 .
.
Отметим, что неопределенный интеграл от непрерывной функции  — множество функций, отличающихся друг от друга на число
— множество функций, отличающихся друг от друга на число 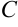 , а определенный интеграл от непрерывной функции
, а определенный интеграл от непрерывной функции  — действительное число.
— действительное число.
Рассмотрим пример вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.
Пример №21.1.
Вычислите 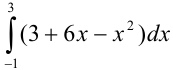 .
.
Решение:
Сначала найдем неопределенный интеграл от заданной функции, выбрав 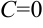 и добавив границы интегрирования:
и добавив границы интегрирования: 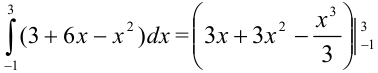 .
.
Подставим сначала верхнюю, потом нижнюю границы интегрирования:
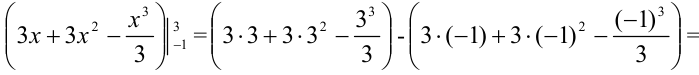
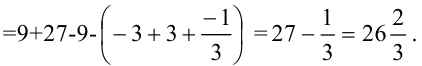
Ответ: 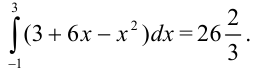
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие определенного интеграла. |
| Основные свойства определенного интеграла. |
| Применение формулы Ньютона-Лейбница. |
| Интегрирование подстановкой (заменой переменной). |

