Оглавление:




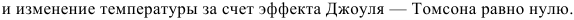

Физические свойства газа.
Физические свойства газа. Состояние однородного газа определяется тремя параметрами: абсолютным давлением p, плотностью, абсолютной температурой T, но только 2 из них являются независимыми. Уравнение, связывающее эти величины Ф (р, Т, Т)= 0, называется уравнением состояния. Уравнение Клапейрона для массы газа m, занимающей объем V, имеет вид、 рv = MRT, в (1.10) Где R-газовая постоянная Дж / (кг•к), измеренная по СИ. Выражение (1.10) также можно записать в виде: п /= РТ. (1.11) Уравнение Клапейрона для 1 киломолд газа C имеет вид、 (1.12)) Где универсальная газовая постоянная является постоянной всех газов и равна 8314 Дж / (кмоль•к). Для воздуха газовая постоянная равна 。 (1.13) Удельный объем gas газа и его плотность связаны следующими соотношениями.
Если давление p, плотность и абсолютная температура T удовлетворяют уравнению Клапейрона (1.11) или (1.12), а удельная внутренняя энергия газа U выражается следующим образом, то газ называется полным. 、 Где cV теплоемкость газа при постоянном объеме. Людмила Фирмаль
- Для реальных углеводородных газов, уравнение состояния выражается как: (1.14) Или 。 (1.15) Здесь; (1.16) Z-коэффициент сжатия. РС, ТС-давление и температура в критической точке, то есть температура, с критическое давление. Критической точкой является точка на изотермической карте (рисунок состояния p-V-T), разность между насыщенным паром и жидкостью disappears. At температура выше критической, двухфазного состояния нет. Вещество находится в монофазном состоянии. Для природных углеводородных газов степень сжатия определяется по экспериментальной кривой. Если параметры, определяющие состояние, остаются постоянными, то система находится в состоянии термодинамического равновесия. Обратимый процесс-это процесс изменения состояния системы, когда она движется в противоположном направлении, проходит через то же промежуточное состояние и возвращается в исходное состояние, без каких-либо изменений в окружающей среде. Обратимый процесс может быть представлен как непрерывная последовательность равновесия states. As квазистатический процесс.
- Уравнение состояния равновесия (1.10)-(1.16) можно использовать при выводе уравнения, описывающего его, только если сам процесс можно считать квазистатическим. Первый закон термодинамики описывает закон сохранения энергии, который применяется для преобразования механической энергии в тепловую и наоборот. Для квазистатического процесса его можно сформулировать следующим образом: основная тепловая энергия dQ, которая подводится к единичной массе газа, расходуется на увеличение внутренней энергии du газа и выполнение работы расширения pd. (1.17) Количество тепла, сообщенное в gasdq, не является полной разницей, поскольку оно зависит не только от начального и конечного состояния газа, но и от процесса изменения состояния. Умножив уравнение (1.17) на интегральный коэффициент 1 / T, получим полную производную функции, которая называется энтропией. 。 (1.18) При переходе газа из состояния 1 в состояние 2 Изменение энтропии s2-S1 не зависит от переходного процесса и определяется только начальным и конечным состояниями.
Для идеального газа (1.19) Где k-cp / cV-адиабатический индекс Пуассона. cf и cV это теплоемкость газа при постоянном давлении и постоянном объеме соответственно и относятся к единице массы. Они измеряются в Дж /(кг•К) С помощью СИ. Людмила Фирмаль
- Приращение энтропии, определяемое формулой (1.19), также присваивается единичной массе. Процессы, протекающие без теплообмена между системой и окружающей средой, называются теплоизоляцией, а процессы, протекающие с постоянной энтропией, называются изэнтропиями. Изоэнтропический процесс описывается уравнением Пуассона-адиабата. Это следует из уравнения (1.19), если S2 = Sl. (1.20) Процесс, который происходит при постоянной температуре, называется isothermal. It описывается уравнением Бойля и Марриотта 。 (1.21) Энтальпия на единицу массы (или количество тепла при постоянном давлении) является функцией (1.22)) Это определяется только состоянием газа, таким как температура и давление. В случае адиабатического течения реального газа через дроссель (клапан, диафрагму и др.) из области высокого давления PI в область низкого давления p2 наблюдается изменение температуры, вызванное изменением давления. Это явление называется эффектом Жюля Томсона. Если начальный расход газа восстанавливается за дросселем, то энтальпия.
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:

