Экстремум функции, недифференцируемой в данной точке.

Экстремум функции, недифференцируемой в данной точке.

• Экстремумы недифференцированной функции в данный момент времени. Выше мы рассмотрели проблему существования экстремумов функции f (x) в точке, где функция f (x) дифференцируема. На данный момент мы не знаем в C, но мы знаем в C в функциях, которые дифференцируемы везде в некотором соседе справа и слева от C, и тем более в C они непрерывны. Оказывается,

теорема 7.1 может быть обобщена в случае таких функций. Чтобы быть точным, делается следующее заявление: Т Е О Р Е М А7. 4. Пусть функция f (x) дифференцируется в любом месте некоторой окрестности точки C, и пусть она непрерывна в точке C, за исключением самой точки C. Тогда, если в заданной окрестности производная f'(x) положительна (отрицательна) слева от точки C и отрицательна (положительна) справа от точки C,

то функция f (x) имеет локальный максимум (минимум) в точке C. Если производная Людмила Фирмаль

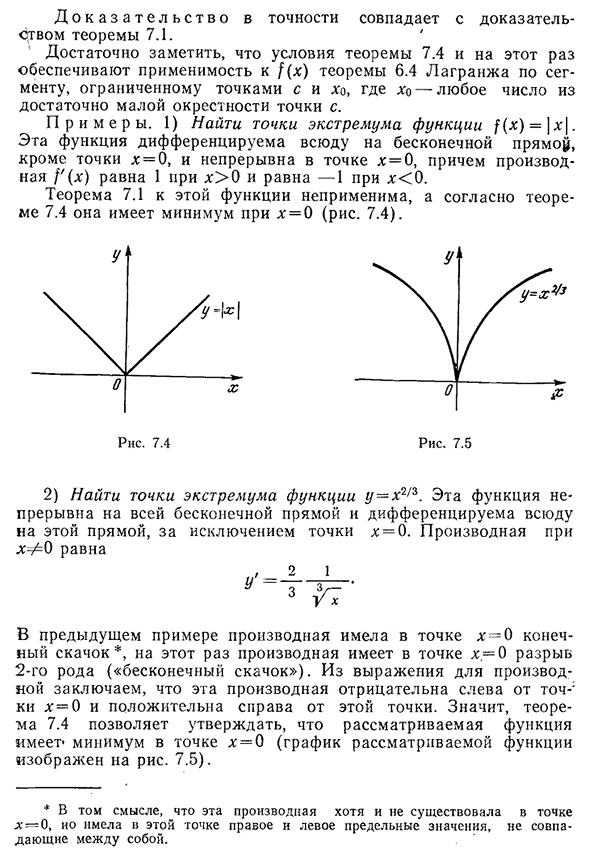
f'(x) имеет одинаковый знак слева и справа от точки C, то в точке C.§1 нет экстремума. Найти стационарную точку 269 Д О К А З а т е л ь с Т В О точно соответствует доказательству теоремы 7.1. Условием теоремы 7.4 и на этот раз является теорема Лагранжа 6.4 для отрезка, ограниченного точками C и XO, где xo-произвольное число из достаточно малой окрестности точек C. P R I m er s. 1) Найти крайнюю точку функции f (x)=/x|. Эта функция дифференцируема везде на бесконечной прямой, за исключением x=0, которая непрерывна при x=0, а производная f'(x) равна 0 при x>1 и -1 при x<0. Теорема 7.1. 1 не

относится к этой функции, и согласно теореме 7.4, x=0(рис. 7.4). Рис 7.5 2) Найти крайнюю точку функции y=x ‘ 2-13. Эта функция непрерывна через бесконечную линию и дифференцируема в любом месте этой линии, за исключением точки x=0. Производная от Х-АО равна В предыдущем примере производная имела конечный скачок в точку x=0*, но теперь ее производная имеет точку x, разрыв 2 типов to=0 («бесконечный скачок») из уравнения производной, эта производная отрицательна слева от точки x=0 и считается положительной справа

• от этой точки. Итак, с помощью теоремы 7.4 можно утверждать, что рассматриваемая функция является наименьшей в точке x=0 (график возможных функций показан на рисунке). 7.5). В смысле этой производной она не существовала в точке l’-0, но имела левое и правое предельные значения, не совпадающие друг с другом в этом отношении.Двести семьдесят я, я … 7. Рассмотрим график функции 3) найти крайнюю точку функции Икс 1+L в х0, П-ф В X O=0. Легко

видеть, что функция бесконечна * прямая и непрерывная во всем. Фактически, единственной «подозрительной» точкой является точка x=0, но даже в этом отношении функция непрерывна. * Вместо интервала (a, B) можно представить бесконечную прямую линию или открытую полулинию. Х-фр-О-О х — >0-0 Кроме того, ясно, что рассматриваемая функция дифференцируема по бесконечным линиям, за исключением точки x=0.

Везде в это время производная определяется по формуле 1-1 ,X, X, X. 1+e+ — e, x Есть~ ——————— т. Людмила Фирмаль

————- • (*) *С-Е п f (x) — f (0) 1 Ограничения Lim — — — — =IIM- — — — — — — — — *легко увидеть, что этого не существует х — «0х х -» 0 — 1+е х Таким образом, функция y=f(x) не известна при x=0. Так как производная y ‘ положительна как слева, так и справа от точки x=0, то рассматриваемая по теореме 7.4 функция не имеет экстремума в точке x=0, поэтому экстремума нет вообще. (График функции показан на рисунке. 7.6.) Рис 7.7

Смотрите также:

Математический анализ онлайн

Условия монотонности функции на интервале	Раскрытие неопределенности вида 0/0
Отсутствие разрывов первого рода и устранимых разрывов у производной.	Раскрытие неопределенности вида ∞/∞.