Оглавление:
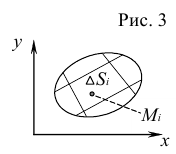
Пусть на замкнутой области 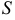 плоскости
плоскости 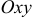 задана непрерывная функция
задана непрерывная функция 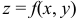 . Разобьем область
. Разобьем область 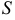 на
на 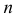 частей
частей 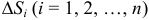 и возьмем точки
и возьмем точки 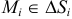 (рис. 3). Составим сумму
(рис. 3). Составим сумму 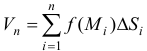 . Эта сумма называется интегральной суммой для функции
. Эта сумма называется интегральной суммой для функции 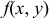 в области
в области 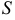 .
.
Двойным интегралом 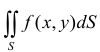 (1) от функции
(1) от функции 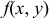 , распространенным на область
, распространенным на область 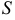 , называется предел интегральной суммы
, называется предел интегральной суммы 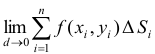 при
при 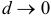 , если этот предел существует и не зависит от способа дробления области
, если этот предел существует и не зависит от способа дробления области 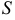 на элементарные ячейки
на элементарные ячейки 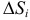 и выбора точек
и выбора точек 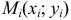 в них; где
в них; где 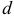 — наибольший диаметр ячеек
— наибольший диаметр ячеек 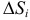 ,
, 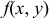 называется подынтегральной функцией,
называется подынтегральной функцией, 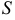 — областью интегрирования,
— областью интегрирования, 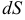 — элементом площади. В прямоугольных координатах
— элементом площади. В прямоугольных координатах 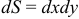 .
.
Геометрический смысл двойного интеграла. Если в интеграле (1) подынтегральная функция 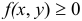 и поверхность
и поверхность 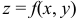 является непрерывной, то двойной интеграл представляет собой объем прямого цилиндра с образующей параллельной оси
является непрерывной, то двойной интеграл представляет собой объем прямого цилиндра с образующей параллельной оси 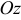 , ограниченного снизу конечной замкнутой областью
, ограниченного снизу конечной замкнутой областью 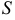 плоскости
плоскости 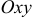 , сверху — поверхностью
, сверху — поверхностью 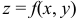 .
.
Двойной интеграл обладает всеми основными свойствами определенного интеграла:
1. Область интегрирования двойного интеграла можно разбить на части
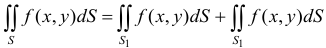 , где
, где 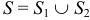 ;
;
2. Двойной интеграл от суммы функций равен сумме двойных интегралов от всех слагаемых
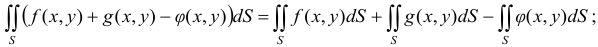
3. Постоянный множитель можно выносить за знак двойного интеграла
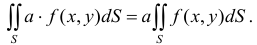
Область 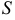 называется стандартной (
называется стандартной (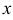 — трапецией) относительно оси
— трапецией) относительно оси 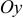 , если она представляет собой криволинейную трапецию (рис. 4):
, если она представляет собой криволинейную трапецию (рис. 4): 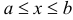 ,
, 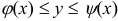 , где
, где 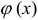 и
и 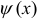 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 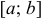 . Причем любая вертикаль, проходящая через точку
. Причем любая вертикаль, проходящая через точку 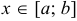 , пересекает границу области
, пересекает границу области 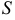 только в двух точках.
только в двух точках.
Область 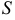 называется стандартной (
называется стандартной (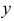 — трапецией) относительно оси
— трапецией) относительно оси 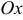 , если она представляет собой криволинейную трапецию (рис. 5):
, если она представляет собой криволинейную трапецию (рис. 5): 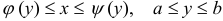 , где
, где 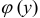 и
и 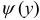 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 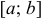 . Причем любая горизонталь, проходящая через точку
. Причем любая горизонталь, проходящая через точку 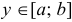 , пересекает границу области
, пересекает границу области 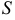 только в двух точках.
только в двух точках.
Вычисление двойного интеграла (1) сводится к вычислению одного или суммы нескольких двукратных интегралов вида 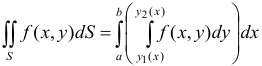 . В этом выражении сначала вычисляется интеграл, стоящий в скобках, причем интегрирование производится по
. В этом выражении сначала вычисляется интеграл, стоящий в скобках, причем интегрирование производится по 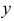 , а
, а 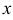 считается постоянным. Как правило, пределы при первом интегрировании являются переменными. Пределы при втором интегрировании всегда постоянны.
считается постоянным. Как правило, пределы при первом интегрировании являются переменными. Пределы при втором интегрировании всегда постоянны.
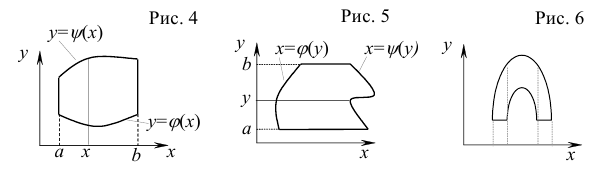
Если область 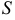 — стандартная относительно оси
— стандартная относительно оси 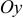 (рис. 4), то двойной интеграл удобно вычислять по формуле
(рис. 4), то двойной интеграл удобно вычислять по формуле 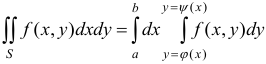 .
.
Если область 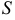 — стандартная относительно оси
— стандартная относительно оси 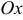 (рис. 5), то двойной интеграл удобно вычислять по формуле
(рис. 5), то двойной интеграл удобно вычислять по формуле 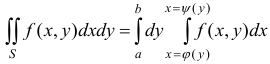 .
.
Если область 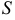 — нестандартная (рис. 6) и ее удается разбить на сумму стандартных областей, то при вычислении двойного интеграла используют его первое свойство.
— нестандартная (рис. 6) и ее удается разбить на сумму стандартных областей, то при вычислении двойного интеграла используют его первое свойство.
Величина двойного интеграла не изменится, если его вычислять сначала по переменной 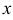 , а потом по переменной
, а потом по переменной 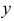 , или наоборот.
, или наоборот.
Пример №1
Изменить порядок интегрирования в двукратном интеграле
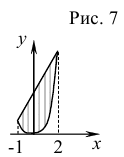
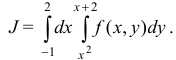
Решение:
Область интегрирования 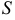 ограничена кривыми
ограничена кривыми 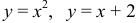 и
и 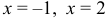 (рис. 7). Отсюда, изменяя роли осей координат, получаем
(рис. 7). Отсюда, изменяя роли осей координат, получаем 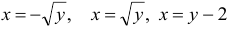 и
и 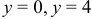 .
.
Следовательно,
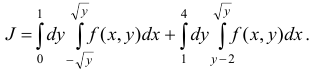
В рассматриваемом примере, поскольку область интегрирования 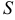 является стандартной относительно оси
является стандартной относительно оси 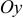 , двойной интеграл
, двойной интеграл 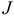 проще вычислять сначала по переменной
проще вычислять сначала по переменной 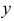 , потом по переменной
, потом по переменной 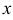 .
.
Для преобразования двойного интеграла, отнесенного к прямоугольным координатам, в двойной интеграл в полярных координатах нужно в подынтегральном выражении прямоугольные координаты заменить полярными: 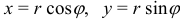 , а вместо
, а вместо 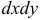 подставить
подставить 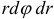 . При этом уравнения линий, ограничивающих область интегрирования, также преобразуются к полярным координатам.
. При этом уравнения линий, ограничивающих область интегрирования, также преобразуются к полярным координатам.
Площадь 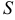 плоской области
плоской области 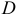 в прямоугольных координатах равна двойному интегралу
в прямоугольных координатах равна двойному интегралу 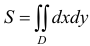 , в полярных координатах —
, в полярных координатах — 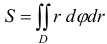 .
.
Масса 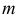 плоской фигуры, занимающей область
плоской фигуры, занимающей область 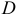 , с поверхностной плотностью
, с поверхностной плотностью 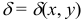 , статические моменты
, статические моменты 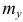 и
и 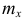 , координаты центра тяжести
, координаты центра тяжести 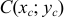 , моменты инерции относительно осей
, моменты инерции относительно осей 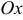 и
и 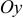 (
(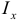 и
и 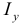 ) и начала координат
) и начала координат 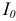 выражаются по формулам:
выражаются по формулам: 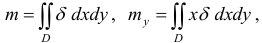
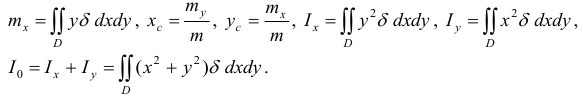
Пример №2
Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах 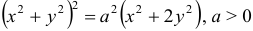 .
.
Решение:
Перейдем к полярным координатам. Полагая в уравнении кривой 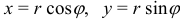 получим:
получим:
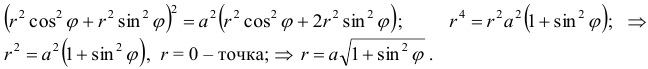
Кривая определена при любых значениях 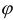 . Найдем площадь, ограниченную кривой по формуле
. Найдем площадь, ограниченную кривой по формуле
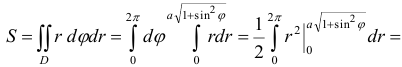
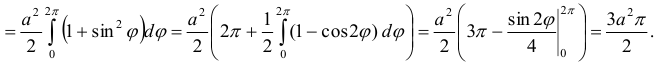
Ответ: 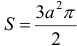 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Наибольшее и наименьшее значение функции z=f(x,y) |
| Метод наименьших квадратов |
| Тройной интеграл |
| Криволинейный интеграл |

