Два режима движения жидкости

Два режима движения жидкости

Два режима движения жидкости. Несмотря на то, что Механика жидкости как область знания существует уже более 1 тысячи лет, идея о двух режимах движения жидкости сложилась только в 19 веке. В 1839 году немецкий исследователь Хаген впервые заметил, что средняя скорость жидкости и вязкость сами по себе влияют на скоростную зависимость потери давления в трубе, а затем, при больших скоростях, в трубе образуется вихревая структура, при малых скоростях движение жидкости происходит слоисто. В Краска а) стеклянная трубка в режиме ламинарного потока 1 Б) режим турбулентности Фундаментальные исследования по режиму течения были проведены британскими учеными в 80-х годах XIX века О.

Это было сделано Рейнольдсом на устройстве, носящем его имя (рис.5.12). в цилиндрическую стеклянную трубу через гладкую коническую входную головку подается жидкость из резервуара и жидкость оседает с помощью сеточной системы. Рисунок 5.12.Устройство Рейнольдса для исследования движения жидкости Окрашенная жидкость плотностью и расходом, близкими к тем же характеристикам, что и поток жидкости в трубе, подается через тонкую трубку на входное сечение трубы. Цветной поток жидкости позволяет визуализировать (визуализировать) структуру потока в трубе. Эксперименты, проведенные на этой установке, показали, что малое значение скорости V приводит к слоистому движению жидкости в трубе.

Так, в ламинарной области происходит ламинарное движение жидкости, траектории движения частиц жидкости выравниваются и определяются контуром твердой границы. Людмила Фирмаль

• Цветная струйка имеет форму нити с четко очерченными границами. Этот режим движения называется ламинарным потоком. При увеличении скорости V ламинарная структура потока разрушается, и движение приобретает совершенно другие характеристики. Красящая жидкость быстро рассеивается по всему потоку. Отдельные окрашенные частицы жидкости движутся по сложной и сложной траектории path. At на небольшом расстоянии от входа (диаметр трубы 10-20) поток равномерно окрашивается. Более детальное исследование показало, что в каждой фиксированной точке пространства скорость жидкости изменяется случайным образом с течением времени. Этот режим движения называется турбулентностью.

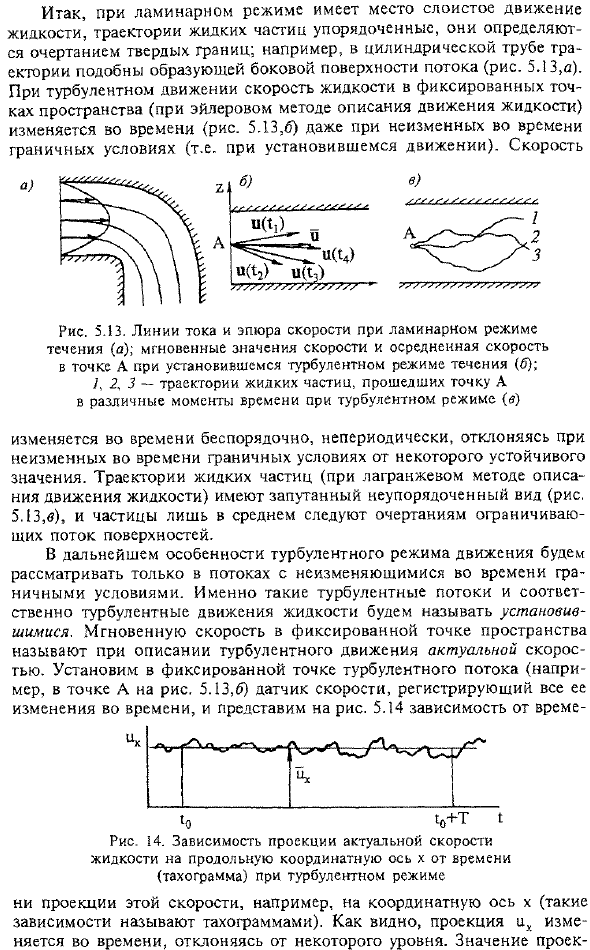
• Например, в цилиндрической трубе траектория подобна шине со стороны потока (рис. 5.13, а). при турбулентном движении скорость жидкости в неподвижной точке пространства(с использованием метода Эйлера для описания движения жидкости) изменяется со временем, даже при инвариантных во времени граничных условиях (т. е. стационарном движении) (рис. 5.13.6).Скорость Случайное, непериодическое изменение во времени, которое отклоняется от определенного стабильного значения в определенное граничное время. Траектория движения частиц жидкости (Лагранжев метод описания движения жидкости) имеет сложный нерегулярный вид (рис. 5.13, В), и частицы следуют только контурам поверхности, которые в среднем ограничивают течение.

В дальнейшем мы будем рассматривать особенности турбулентного режима движения только в потоках с инвариантными по времени граничными условиями. Такие турбулентные и соответственно турбулентные движения называются стационарными. Мгновенная скорость в неподвижной точке пространства называется действительной скоростью при описании турбулентности motion. In фиксированную точку турбулентного потока (например, точку а на рис. 5.13.6), фиксируют все изменения во времени и устанавливают датчик скорости, показанный на Рис.5. 5.14 зависит от времени 10 10 + Т Я Рис.14.Зависимость проекции действительной скорости жидкости от времени (тахограмма) в турбулентном режиме на оси ординат x.

Если вы решите из аналогичной зависимости для всех трёх проекций средней скорости, вы можете построить вектор средней скорости в определенной точке пространства, занятого потоком Людмила Фирмаль

• Также проекция этой скорости осуществляется, например, по осям x (такая зависимость называется тахограммой). как видим, их проекция изменяется со временем и отклоняется от определенных уровней. Стоимость проекта-102 Определите местоположение этого уровня, скорость ССС、 (5.74） Их p (0 ^» 1л То есть равна высоте прямоугольника, который является такой же площадью фигуры на рисунке 5. 14, расстояние t с такограммой ограничено вертикальной линией только далеко. Значение T должно быть таким, чтобы значение, вычисленное по выражению (5.74), не зависело от T.

In кроме того, они называются средними проекциями скорости. (5.74) : u〜(u, u, u2). Конечно, вы можете выполнить ту же операцию усреднения в любой точке системы. flow. In в частности, например, на рисунке 5.13.5 показан поток жидкости в цилиндрическом канале. Стенки формируются параллельно x-axis. In в этом случае средняя скорость в любой точке потока U (x, y, r) имеет только 1 проекцию из них. Это не ноль, а yu = 0 и u2-0.In в других, более сложных случаях все 3 проекции средней скорости могут быть ненулевыми. Конечно, гидродинамическое давление в точке р, которое изменяется при турбулентном движении.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Потенциальный и полный (гидродинамический) напоры. Пьезометрическая и напорная линии.
2. Основное уравнение равномерного движения жидкости.
3. Потери напора при установившемся равномерном движении жидкости (потери по длине).
4. Формула Шези.