Дополнительные члены приближенных формул

Оглавление:

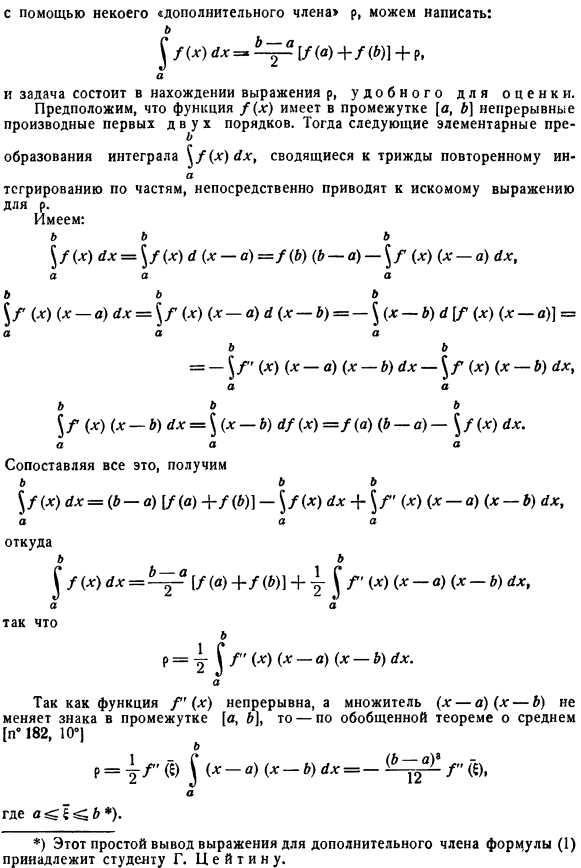
Дополнительные члены приближенных формул

Дополнительные члены приближенных формул. Во-первых, подумайте о простейшем частном случае формулы трапеции, которая соответствует предположению 1, То есть Формуле(1). Восстановите точность этого выражения С помощью»дополнительных членов» p, вы можете написать: б $ / (х) топор =.^ [/©+ / ( » )] + п Но… И задача состоит в том, чтобы найти выражение p, которое удобно для вычисления. Предположим, что функция/(x) имеет непрерывную производную Первого 2-го порядка интервала[c, b].Затем следует следующее основное продвижение б Формирование интеграла^ / (x) 4x>это повторяется 3 раза Но…

Для каждой части это непосредственно приводит к желаемому представлению р. Этот простой вывод уравнения из дополнительного члена уравнения (1) принадлежит Цейтину. Людмила Фирмаль

У нас есть： б, б. \ /(х) ух = \ /(х) 1 {х-а)= ф (б) {б-а) \ р(х) (х-а) (Х-а) т、 ля. \ р(х) (х-а) топор = \ р (х-о) (х-б)=-(х-б) \ т (х) (*а)] = A а、 б = $/«(Х) (х-а) {х-б) топор \ р(х) (х-б) топор、 Но、 б, б. $ Ф *(Х) (х-б) 4х = т(х-б) / ( * ) = ф(А)(Б-А) $ /(х) 4х. ля. Если вы сравните все это, б \ /(х) топор =(Б-А)\ /(А)+ / (Б) -\ /(г)ах + \ р(х) (х-а)(х-б) топор. Откуда б ^ /(х:) аж = ^ [/(а)+ / ( & )] + г!| Р(х) (х-а) (х-б) о、 р = г | / «(х) (х-а) (х-б) ах. Так как функция f (x) непрерывна и фактор (x-a) (q-b) не изменяет знак на интервале[a, 6), то обобщенная теорема о среднем[n * 182,10°| б Р =(1)| (х-а) (х-б) топор =Но… ля.)^§ Если интервал[a, b \разделить на равные части n> 1, то для каждого доказанного деления[x^,•+.) получим точную формулу. $ /(х) DX = ^ * 21 + ±^1 _Y(€|.(Λ|.^ е ХС + 1).

Эти уравнения (/=0, 1,…если вы добавляете n-1) за термин, это выглядит так: б ^ ^ = 4м3 + а + * • * + Л.)+*». Но… (Л = 6-л） Где это выражение r, гамма (eo)+Гамма 6)+.. +Γ 12l8 * л Существует также дополнительный член в Формуле трапеции(3). Непрерывная функция интервала[l, b] [n°73]/ » (x) минимальное и максимальное значения m и A соответственно! А потом среднее арифметическое ■ Г (6^®)+Г (6″ −1> л Из-за известных свойств непрерывной функции (n * 70), [l, b\, упомянутая формула является/(?Есть точки, которые точно равны).Поэтому, в конце концов Ка = ШГ^®(7） 1. L5 по мере увеличения l этот дополнительный член приблизительно уменьшается. Г-ых ！1 + * » 1. Произведенный Например, вернемся к вычислению интеграла данные для n * 189.In случай подынтегрального выражения, f (x) -.

Эта производная от интервала [0, 1] меняет знак, но、 (1×1） Абсолютное значение остается меньше 2.Отсюда выражение (7) по| /?»Около I 0.0017. Мы вычислили 0. 00005 ордината с точностью до 4 digits. It Истинная ошибка на самом деле меньше, чем эта граница. Ограничивается тем, что относится к формуле Симпсона (6>), дающей дополнительные члены без вывода. * ) E также говорит примерно, потому что он может измениться с L change. It необходимо это отметить. Н 180.(2л） 7 / N) (1） Б). (8） Для функции f (x) из 4 последовательных производных этот дополнительный член (если интервал разбить на 2n частей) будет иметь следующий вид.

Г-ых Опять же, чтобы избежать интеграла 1 m-rВ + Х Число производных 4-го порядка, входящих в уравнение(8)、 Поскольку функция f (x)= ^ x%сама по себе является производной от y = amc \%x、 что вы можете использовать готовую формулу от l°9b, 5).Я с ней согласен. / 4>(х)= г {Б)-24 $ 5У $ 1Н 5 [г + ^}、 где I / 4CH *) I ^ 24, отсюда выражение (7) по| [^^ 0.0006.Правда. как ная error. It оказывается, она значительно меньше этой границы. Examples. In заключение поставлена задача вычисления эллиптического интеграла 2-го рода ( * ) до 0,001 по формуле Симпсона для приведения примера приближенного вычисления конкретного интеграла, значение которого заранее неизвестно. У нас есть Ням К (Т) ’ Сто восемьдесят ^ * 12 т-(2Г)’ -как(| Г 10Функция/ ( * ) = » 1—b * * d: Когда x изменяется от 0 до 1^（■*）（12 **）、итак [см. (7)] * ) Полнотой называется Интеграл Γ (k, γ) и E(k, y) ружандра.

Нетрудно заметить, что погрешность, обусловленная округлением ординаты, включена в приведенные выше оценки. Людмила Фирмаль

Я =В этом случае опустите 2-й аргумент нотации Просто напишите E (k), E(k).Существует специальная таблица для полной интеграции. * * ) Очевидно,= = f (x) ETA=; дифференциация идентичности ^ Р 2 г * = 1-y81n * ЛГ、 Легко получить непрерывную верхнюю оценку абсолютного значения производной/, y», y ’»9 y’ ’»\ Мне все еще нужно добавить Коррекция (неотрицательная), за исключением коррекции округления、 0.00003. Подобный этому 1.35118、 Итак, возьмем 2n = b / / 0,00052.И затем… = 0 (0 -).У0 = 1,0000 Я −12 (15 )4 года,/ a = / 12 + / Г2= 3,9324 Я T (30) 2 года,= / T4 / 2 = 1.8708 *•/.Я «T (45 *) 4 года/ / = L2 = 3,4641 Х * я ~ ~ 3 (60 -) 2 года,= / 10/2 = 1.5811 ** / , 5 дней «12 (75 *)4U5/, = = / 12-U12 =: 2.9216 Я «»2 (90-х)л = / 2/2 = = 0.7071 Сумма 15,477. Семьдесят один 15,4771 ТГ 1,35063… 1.35011 е [ 1/2、 И можно утверждать, что^ = 1.351±0.

Формула трапеций.	Определение понятия площади.
Параболическая формула.	Аддитивность площади.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.