Задача 1.87.
Для задачи, состоящей в определении максимального значения функции
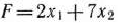
при условиях
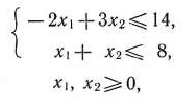
составить двойственную задачу и найти решение обеих Задач.
Решение:
Двойственной задачей по отношению к исходной является задача, состоящая в определении минимального значения функции
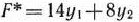
при условиях
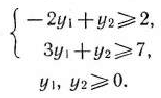
Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию задачи линейного программирования (рис. 1.14 и 1.15).
Как видно из рис. 1.14, максимальное значение целевая функция исходной задачи принимает в точке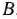 
. Следовательно, 
является оптимальным планом, при котором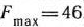 
.
Минимальное значение целевая функция двойственной задачи принимает в точке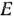 
(рис. 1.17). Значит, 
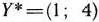является оптимальным планом двойственной задачи, при котором 
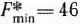. Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.
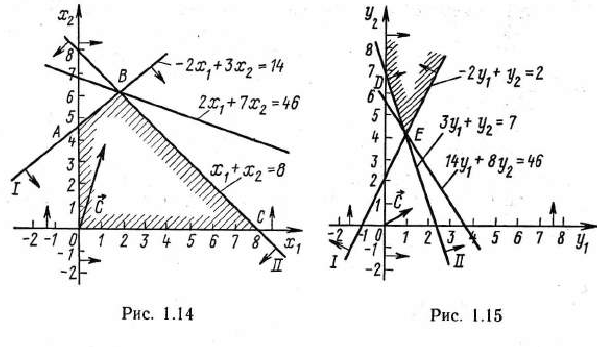
Из рис. 1.14 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис. 1.15, значение целевой функции двойственной задачи при любом ее плане не меньше 46. Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи при ее произвольном плане.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
