Задача 1.78.
Для задачи, состоящей в максимизации функции
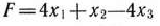
при условиях
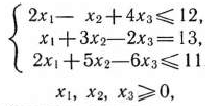
сформулировать двойственную задачу.
Решение:
Для данной задачи
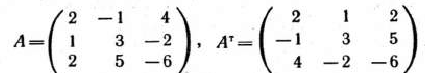
В соответствии с общими правилами задача, двойственная по отношению к данной, формулируется следующим образом: найти минимум функции
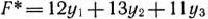
при условиях
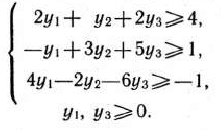
Связь между решениями прямой и двойственной задач.
Рассмотрим пару двойственных задач, образованную основной задачей линейного программирования и двойственной к ней. Исходная задача: найти максимум функции
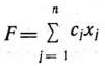
при условиях
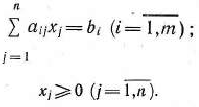
Двойственная задача: найти минимум функции
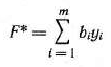
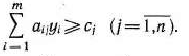
Каждая из задач двойственной пары (61) — (63) и (64), (65) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1.1. Если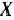 
— некоторый план исходной задачи (61) — (63), а 
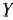— произвольный план двойственной задачи (64), (65), то значение целевой функции исходной задачи при плане 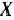всегда не превосходит значения целевой функции двойственной задачи при плане 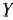, т. е.
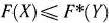
Лемма t.2. Если
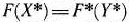
для некоторых планов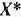 
и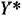 
задач (61) — (63) и (64). (65), то 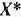— оптимальный план исходной задачи, а 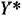— оптимальный план двойственной задачи.
Теорема 1.9 (первая теорема двойственности). Если одна из пары двойственных задач (6i) — (63) или (64), (65) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е.
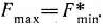
Если же целевая функция одной из пары двойственных задач не ограничена [для исходной (61) — (63) —сверху, для двойственной (64), (65) — снизу!, то другая задача вообще не имеет планов.
Теорема 1.10 (вторая теорема двойственности). План
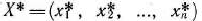
задачи (61) — (63) и план
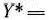
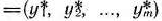
задачи (64), (65) являются оптимальными планами этих задач тогда и только тогда, когда для любого
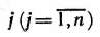
выполняется равенство
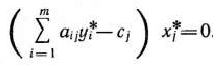
Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев: I) обе задачи имеют планы; 2) планы имеет только одна задача; 3) для каждой задачи двойственной пары множество планов пусто.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
