Пример задачи 6.1
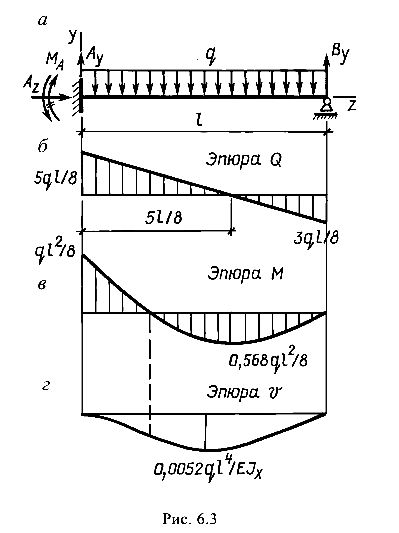
Для балки (рис. 6.3, а) построить эпюры поперечных сил и изгибающих моментов и определить прогиб посередине пролета. Изобразить ось изогнутой балки.
Жесткость сечения балки 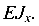
Решение
На левой опоре балки — защемлении (заделке) — возникнут три реакции 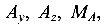 на правой — шарнирно-подвижной — одна,
на правой — шарнирно-подвижной — одна, 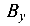 . Всего — четыре реакции. Уравнений равновесия можно составить только три
. Всего — четыре реакции. Уравнений равновесия можно составить только три 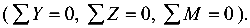 Значит, рассматриваемая балка является один раз статически неопределимой.
Значит, рассматриваемая балка является один раз статически неопределимой.
Составим уравнения равновесия:
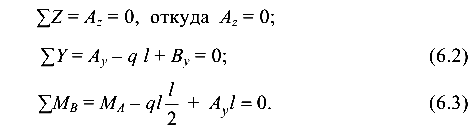
Два уравнения равновесия содержат три неизвестные величины. Непосредственное решение уравнений невозможно.
Необходимо составить одно дополнительное уравнение, исходя из условий деформации на опорах балки: на опоре А угол поворота сечения 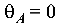 , прогиб
, прогиб 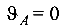 ; на опоре В прогиб
; на опоре В прогиб 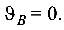
Используем условие на опоре В и составим выражение для определения прогиба 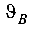 по методу начальных параметров:
по методу начальных параметров:
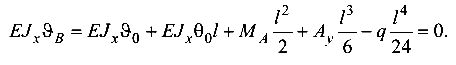
Учтем, что на опоре 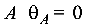 и
и 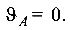 Следовательно, начальные параметры уравнения прогибов
Следовательно, начальные параметры уравнения прогибов 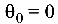 и
и 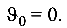
Тогда
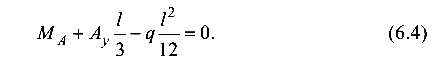
Решив совместно уравнения (6.3) и (6.4), получим
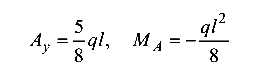
(направление противоположно изображенному на рис. 6.3, а).
Реакцию 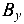 целесообразно определить из уравнения
целесообразно определить из уравнения 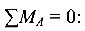
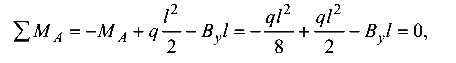
откуда 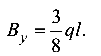
Проверим правильность решения по уравнению (6.2).
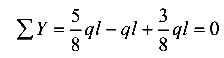 — решение верно.
— решение верно.
После раскрытия статической неопределимости дальнейший расчет балки ведется как и для статически определимой. Эпюры Q и М показаны на рис. 6.3, б и в.
Выражение для определения прогиба посередине пролета балки 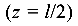
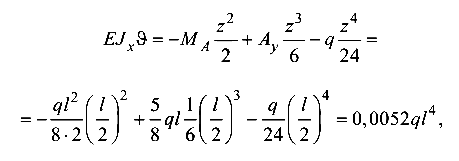
откуда прогиб
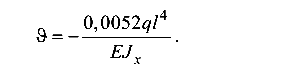
Ось изогнутой балки (эпюра прогибов) изображена на рис. 6.3, г. Напомним, что эпюра прогибов в точке, где М = 0, имеет перегиб
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
