Задача №81.
Для балки (рис. 3.45, а) определить реакции опор в точках 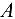 и
и 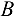 , если
, если
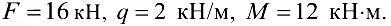
Решение:
Рассматривая равновесие балки, освобождаем точки 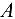 и
и 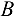 от связей и заменяем связи силами реакций связей
от связей и заменяем связи силами реакций связей 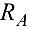 и
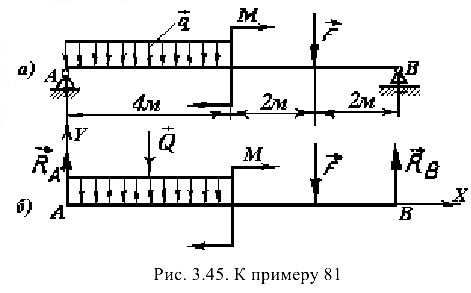
и 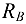 (рис. 3.45, б). Действие па балку равномерно распределенной нагрузки интенсивности
(рис. 3.45, б). Действие па балку равномерно распределенной нагрузки интенсивности 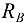 заменяем равнодействующей
заменяем равнодействующей 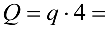 2-4 = 8 кН, которая расположена в середине участка действия этой нагрузки (рис. 3.45, б).
2-4 = 8 кН, которая расположена в середине участка действия этой нагрузки (рис. 3.45, б).
Таким образом, на балку действуют пара сил с моментом 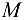 и система параллельных сил
и система параллельных сил
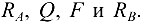
Для определения неизвестных реакций связей балки 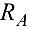 и
и 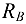 используем уравнения равновесия
используем уравнения равновесия
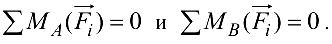
В качестве проверочного уравнения принимаем уравнение
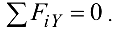
Выберем систему координат 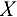 и
и 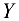 с началом в точке
с началом в точке 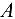 и составим уравнения равновесия сил:
и составим уравнения равновесия сил:
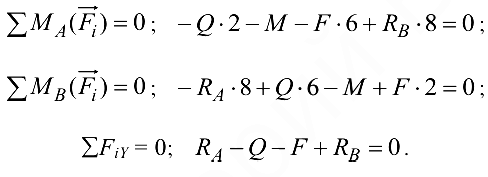
Из уравнения (3.13)
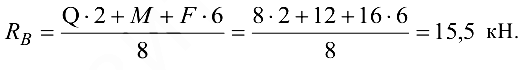
Из уравнения (3.14)
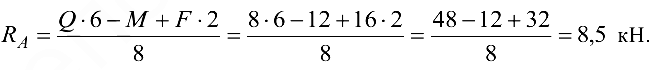
Из уравнения (3.15) следует, что 8,5 — 8 — 16 + 15,5 = 0, следовательно, реакции 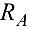 и
и 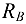 балки по величине и направлению определены верно.
балки по величине и направлению определены верно.
Следует отметить, что момент 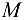 в отличие от сил не изменяет своего знака относительно точек
в отличие от сил не изменяет своего знака относительно точек 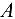 и
и 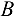 балки (и других произвольных точек) при написании уравнений моментов сил.
балки (и других произвольных точек) при написании уравнений моментов сил.
Ответ:
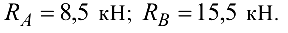
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

