Число e
Используем приведенные в пункте 2 свойства пределов для определения важного в анализе числа е.
Рассмотрим последовательность
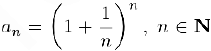
и докажем, что она сходится. Заметим, прежде всего, что
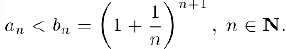
Покажем, что последовательность 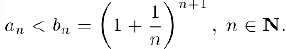является убывающей. Действительно,
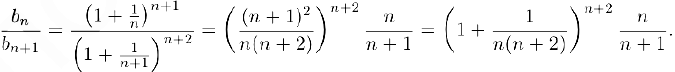
Воспользовавшись неравенством Бернулли (§1). получим:
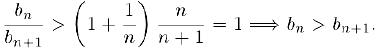
Таким образом, последовательность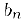 
убывает. Аналогично проверяется, что последовательность 
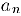является возрастающей. Последовательность 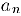ограничена сверху, а 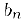— снизу, так как 
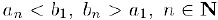. Следовательно, по свойству 4) предела последовательност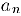и и 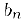сходятся, причем сходятся они к общему пределу, так как благодаря свойству 7). b) предела произведения последовательностей
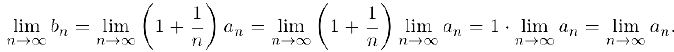
Определение,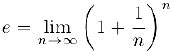 
Пользуясь неравенством (1), мы можем указать сколь угодно малый интервал, в котором содержится число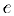 
и, таким образом, вычислить его с любой точностью. Например, уже при 
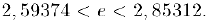
Болес точные вычисления показывают, что
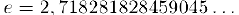
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
| Предел последовательности |
| Свойства и доказательство пределов последовательностей |
| О неопределенностях, возникающих при вычислении пределов |
| Числовая функция и некоторые ее элементарные свойства |
