Оглавление:











Чистый сдвиг
- Чистый сдвиг При расчете многих конструктивных элементов возникает частный случай плоского напряженного состояния, когда на четыре грани прямоугольного элемента действует только касательное напряжение (см. фиг. 183, а). Это напряженное состояние называется Чистым сдвигом. Рассмотрим величину и направление главных напряжений в таких напряженных условиях. Для этого
используют структуру круга напряжений(рис. 183. В этом случае OA==0; tAs _ 1as с _ _ _ тг она _ г€- «г- _ «2 5″ » ~ 2 2 » • По закону крючка для чистого сдвига y= — so Е-2КВ— (8.8) Тогда воспользуемся обобщенным законом крюка (формулы (6.29) J).Основное напряжение Щ действует в направлении диагонали переменного тока.
Поэтому относительное удлинение e диагонали не больше, чем основное Людмила Фирмаль
удлинение EJ при плоском напряженном состоянии, представленном чистым сдвигом. Учитывая зависимость(8.4), из первого выражения (6.30) получаем e= * e,= — L E. видно, что t.to. если сравнить выражения (8.9) (8.8) и (8.9), то вы получите необходимые зависимости: (8.10)) В p=| / -4—получаем G — (0,375 4-0, 4) E. Давайте напишем выражение для перемещения одной грани относительно другой (абсолютный сдвиг As) в чистом сдвиге. Результирующая сила сдвига Q-Ft, указывающая площадь плоскости F, и расстояние между гранями, подлежащими сдвигу (рис. 184), получаем Т Оа а=уа-а= , То есть (8.11) Формула (8.11)представляет закон крюка для абсолютного сдвига. Энергия потенциальной деформации рассматриваемого элемента при чист
ом сдвиге С-и-2-2GF’ И с определенной потенциальной энергией (?)Но _ И~V~2GF■aF2F-G’ То есть Испытание прочности и допустимого напряжения при чистом сдвиге. Проверим прочность элементов, испытавших чистую деформацию сдвига(рис. 183, а). Тангенциальное давление поверхности элемента равно t, допустимое давление для материала, находящегося под напряжением, равно[o|. Как уже упоминалось выше, основное напряжение при чистом сдвиге Oh=t; og=0; O3= — T. Условия интенсивности определяются второй, третьей и четвертой теориями:а)второй теорией < (°1-(8.13) Подставляя
- значение основного напряжения, можно увидеть Восемь -“ ) Правая часть уравнения (8.14)представляет допустимое напряжение для чистого сдвига: М-Ттит- С=0,25 для металла 4-0. 42. Поэтому, согласно второй теории прочности 1T)=(0,7 4-0, 8) [o]; (8.16)b) согласно третьей теории прочности, o » — oz<1<и, Или т-(-т)<[о], Откуда (8.17)) То есть допустимое напряжение сдвига[t]=0,5[I]; В) согласно четвертой теории прочности 200внеся значение основного напряжения получаем (8.19) И так оно и есть., [т]= — м- » 0,6[а]. (8.20)значение результирующего допустимого напряжения также используется для расчета прочности деталей, подвергнутых сдвиговой деформации (болты, заклепки, ключи и т.д.).да что с тобой такое? Отметим, что наиболее подходящая формула для пластического материала (8.20) получена на основе четвертой теории прочности. При использовании этой формулы
необходимо принять текущее значение допустимого напряжения растяжения. Например, для стали марки СТЗ допустимы растягивающие напряжения и сжатие о=1600кгф/ ‘ см2. Затем [t]=0,6•1600=960 кг / см2″1000 кг / см2. Условия прочности на сдвиг (сдвиг) могут быть записаны в обычном виде: Tiax= — V — < < 8>2.) Величина допустимых напряжений в сечении [t] зависит от характеристик материала, характера нагрузки и типа конструктивных элементов. Причина выбора допустимого напряжения[t]такова, как указано выше, и значение допустимого напряжения сдвига для некоторых
материалов, связанных с заклепками и сварными швами, показано в таблице 11. В качестве Людмила Фирмаль
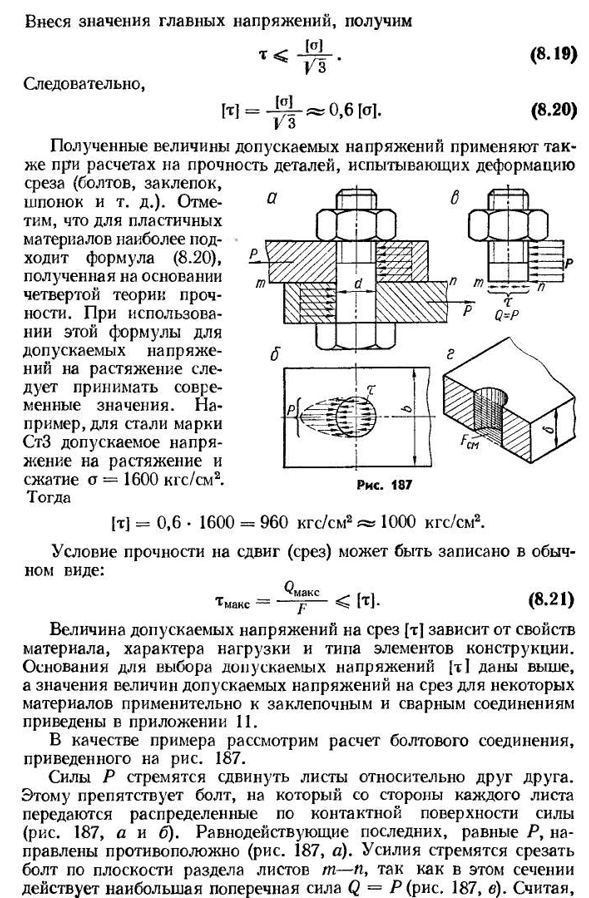
примера рассмотрим расчет болтового соединения, как показано на рисунке. Сто восемьдесят семь Сила p стремится сдвинуть листы друг против друга. Это предотвращается болтами, и сила, распределенная по контактной поверхности, передается со стороны каждого листа(рис. 187, а и Б). Равнодействующая сила, равная Р, находится в противоположном направлении фиг. 187, а). Усилия действуют так, как в этом сечении действует максимальная боковая сила Q=P, которая стремится отсоединить болты на плоскости сопряжения листа t-P9(рис. 187, в). Думать., Что касательное напряжение равномерно распределено Я здесь. Четыре. Таким образом, условие прочности на сдвиг Болта принимает вид ^ф-ф-ф-ф г] О! Рис сто восемьдесят девять Сила скобок N 22, например. Для
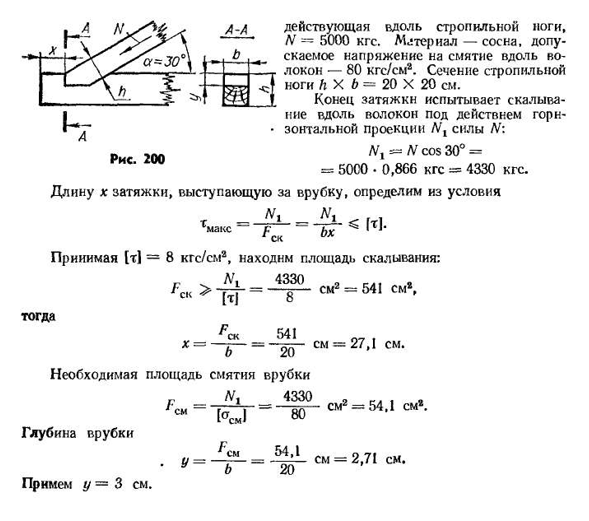
определения необходимого количества заклепок диаметром d-23 мм, на листе (шарфе) в форме толщиной b=1,2 см(рис.189) с подкосами ферм, состоящих из двух углов 90Х56Х8). Растяжимое=30ТС, материал-СТЗ, отверстие заклепки отжато. Предполагая, что силы между заклепками распределены равномерно, число заклепок i определяется из условий прочности на сдвиг: Н Или смять от состояния силы ИА: Принимая во внимание, что для стали N g1°cm2 можно принять[t]=1000 кгс/см2 и[20, двухпартийный на конце (Х-образные швы, фиг.191, в). Расчетная толщина шва такая же, как и толщина листа в, приток не учитывается. Если листы параллельны или перпендикулярны, то соединение производится с помощью угловых швов. Это коленный сустав- В 204ку, наложение и бренд. Е
сли направление углового шва перпендикулярно рабочей силе, то шов называют передним(краевым). Шов, параллельный силе, называется боковым (side). Косые швы также используются(см. рис. 192), направленный под углом к силе. Для риса. На рисунке 193 показано соединение сидений, перекрывающее передний шов схемы. 194-соединение со сварной накладкой с помощью фланцевых швов, а также рисунок. 195-тройник- Расчетная длина шва. Нене. Если не учитывать приток, то в части углового шва он имеет форму
равнобедренного треугольника (рис. 196, а). Разрушение шва, его минимальное сечение ABCD(фиг. 196, б), его высота a-6cos45E » 0,7 6. Расчетная площадь поперечного сечения шва F3= = al=0,76 Z, где I сварные соединения и заклепки условно рассчитываются исходя из предположения равномерности распределения напряжений по поперечному сечению шва. За столом. 12. приведены некоторые значения допустимых напряжений сварных соединений. Данные в этой таблице могут быть использованы только для структур, созданных STZ. Не останавливаясь на расчете всех видов швов, рассмотрим пример расчета только передних и боковых., Таблиц
а 12 Тип напряжения тока Допустимое значение напряжения Допустимое напряжениекгс / см2 Руководство по эксплуатации сварочного электрода печи покраска Автоматическая сварка и ручная сварка с толстым покрытием электрода Протяжение [OE ] 1000 1300 Сжатие 1100 1450 Срез 1y1 800 1100P R I m e h a n I e. индекс » e » означает, что изделие сваривается электрической дугой. Он должен в первую очередь сопротивляться действию касательного напряжения. 197), учитывая, что сопротивление стали резанию ниже, чем натяжение, компонент нормального напряжения в лобовом
шве пренебрегается, и поперечная нагрузка распределяется равномерно по площади поперечного сечения. В данном случае, о внахлестку в расчет 205вводят оба шва-верхний и Нижний. Тогда будем считать, что оба шва будут работать с общей площадью опасного участка G9=2a1t==20,76/t=1,4 6/t, где 1T-расчетная длина концевого шва、: TJ — < W — ’<8 ′ 26> Качество шва ухудшается в начале и конце шва из-за отсутствия калибровки, поэтому его фактическая длина увеличивается на 10 мм по сравнению с расчетной длиной. I= / t+10 мм, где I-фактическая длина шва(рис. 197/=Б). Из-за незначительной деформируемости материала шва
в направлении действия силы, передний шов является жестким, поэтому он решается с очень малыми остаточными деформациями и может быть повторно переменной и ударной нагрузкой. На самом деле, шов на фланге более распространен. Они вязкие, так как разрушаются только после значительной остаточной деформации. Фланговые швы всегда располагаются попарно; эти швы Работа на участках биссектрисного сечения(рис. 198). Площадь каждого края шва =0.76 (з-10). Требования к прочности на сдвиг принимают форму T=1,46< / −10)1b/m)……………………………………….. Чипирование в разрезы вдоль нитей и Кон зазубрин в пересекает з г и Б………………………………………………………. Сколы в и з г и б е…………………………..
Смотрите также:
| Примеры проверки прочности | Напряжения и деформации при кручении. условия прочности и жесткости |
| Сдвиг. расчет на срез | Анализ напряженного состояния и разрушения при кручении |

