Оглавление:
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина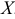 
задана законом распределения вероятностей:
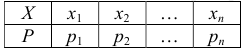
Тогда математическое ожидание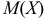 
определяется равенством:
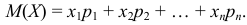
Математическое ожидание дискретной случайной величины есть неслучайная величина (постоянная).
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины:
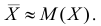
На числовой оси возможные значения расположены слева и справа от математического ожидания. Поэтому его часто называют центром распределения.
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной:
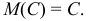
2. Постоянный множитель можно выносить за знак математического ожидания:
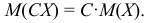
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
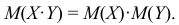
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
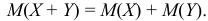
Теорема 1. Математическое ожидание 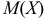числа появлений события 
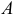в 
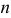независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытания при условии, что в каждом испытании вероятность появления события 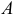равна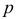 
:
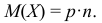
Пример №1
Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по одному билету равна 0,3.
Решение:
Число независимых испытаний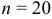 
. В каждом испытании вероятность выигрыша 
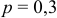. Искомая математическое ожидание:
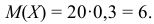
Пример №2
Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей.
Решение:
Обозначим число очков, которое может выпасть на первой кости, через 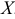и на второй — через 
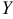. Запишем закон распределения числа очков для первой игральной кости
Найдем математическое ожидание числа очков, которые могут выпасть на первой кости:
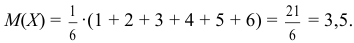
Очевидно, что и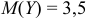 
.
Искомое математическое ожидание
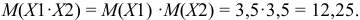
Переход от 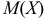к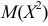 
а тем более к 
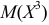и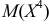 
позволяет лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Для этого используют начальные и центральные моменты.
Начальным моментом порядка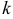 
случайной величины 
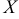называют математическое ожидание величины 
.
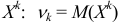Центральным моментом порядка к случайной величины 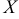называют математическое ожидание величины 
.
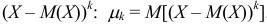В частности,
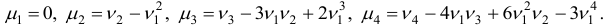
Математическое ожидание отклонения равно нулю:
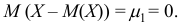
Поскольку математическое ожидание отклонения равно нулю, то для определения степени рассеивания случайной величины вокруг её математического ожидания выделяют среднее значение квадрата отклонения.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
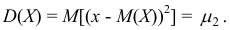
Теорема 2. Дисперсия равна разности между математическим ожиданием квадрата случайной величины 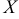и квадратом её математического ожидания:
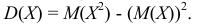
Свойства дисперсии
1) Дисперсия постоянной величины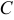 
равна 0: 
.
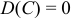2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: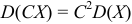 
.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсии этих величин: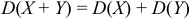 
.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсии этих величин: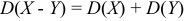 
.
Пример №3
Найти дисперсию случайных величин, зная закон её распределения:
Решение:
Найдем математическое ожидание случайной величины :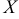
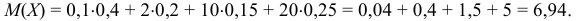
Найдем математическое ожидание случайной величины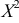 
:
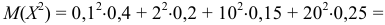
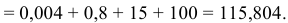
Найдем дисперсию:
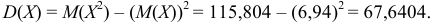
Пример №4
Дискретная случайная величина 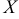имеет только два возможных значения: 
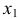и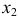 
, причем 
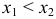. Найти закон распределения величины 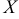, если известно, что 
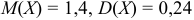и вероятность 
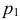того, что 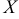примет значение 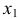равна 0,6.
Решение:
Сумма вероятностей всех возможных значений 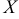равна единице, поэтому вероятность 
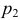равна 1 — 0,6 = 0,4. Итак, закон распределения случайной величины 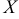имеет вид:
Для отыскания 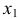и 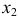составим два уравнения. Учитывая, что по условию 
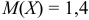, запишем первое из уравнений: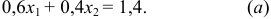 
Принимая во внимание, что по условию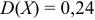 
, используя формулу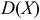 
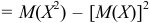, напишем второе уравнение: 
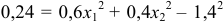, или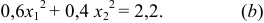 
Решив систему уравнени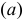й 
и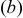 
, найдем два решения: 1) 
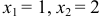и 2)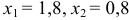 
. По условию 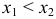, поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения:
Теорема 3. Дисперсия числа появлений события 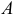в 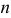независимых испытаниях, в каждом из которых вероятность 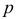появления события постоянна, равна
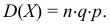
Средним квадратическим отклонением случайной величины 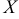называют квадратный корень из дисперсии: 
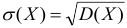. Размерность 
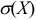совпадает с размерностью .
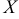Теорема 4. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно:
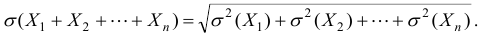
Пример №5
Испытывается устройство, состоящее из трёх независимо работающих приборов. Вероятности отказа приборов таковы: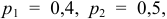 
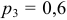. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение числа отказавших приборов.
Решение:
Вероятность того, что ни один прибор не откажет:
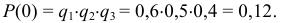
Вероятность того, что один прибор откажет:
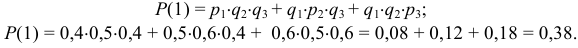
Вероятность того, что два прибора откажут:
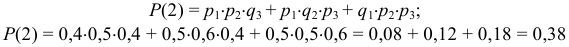
Вероятность того, что три прибора откажут:
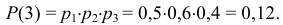
Проверка: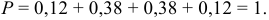 
Запишем закон распределения числа отказавших приборов:
Найдем математическое ожидание случайной величины :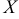
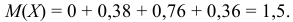
Найдем математическое ожидание случайной величины :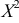
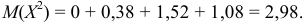
Найдем дисперсию:
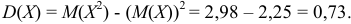
Найдем среднее квадратичное отклонение числа отказавших приборов:
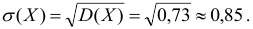
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:
