Частотные характеристики турбулентности

Частотные характеристики турбулентности

Частотные характеристики турбулентности. При объяснении понятия турбулентности, например, было показано, что скорость жидкости при турбулентном движении имеет 3 основных свойства. Среднее значение скорости, характерное значение пульсационной скорости (стандартное), характерное значение частоты пульсационной скорости. Пульсация скорости нерегулярна и нерегулярна(ее нельзя выразить как сумму гармонических колебаний), тем не менее, она обычно может указывать на характерную частоту(или диапазон частот).Например, предположим, что временная шкала вдоль горизонтальной оси принимает тахограмму скорости установившегося движения 1 см = i С, и без изменения формы тахограммы временная шкала I см равна 1 минуте.

Это называется функцией спектральной плотности продольной пульсационной скорости или энергетическим спектром продольной пульсационной скорости. Людмила Фирмаль

• Если сравнить 2 такие тахограммы, то они определяют одну и ту же среднюю скорость, один и тот же критерий скорости пульсации, но заметим, что изменение скорости во времени этих тахограмм различно. В предыдущем разделе было указано, что частотная характеристика может быть оценена по временной корреляционной функции, в частности, временная шкала интегрирования может быть интерпретирована как среднее время, в течение которого скорость пульсации имеет постоянный знак. Однако удобнее анализировать не саму корреляционную функцию, а ее преобразование Фурье (то есть результат преобразования Фурье корреляционной функции). Это преобразование существует, потому что Ki (m) обычно стремится к нулю, как только mw.

От (19.16) Выражение-ri [2 можно интерпретировать как плотность распределения. Поток кинетической энергии обусловлен пульсацией продольной скорости; поэтому уравнение (19.18) допускает следующую интерпретацию функции 8n(w): если действительное изменение скорости во времени выражается суммой гармонических вариаций скорости на разных частотах, принимая значение от 0 до oo, то функция 5P определяет распределение энергии импульса продольной скорости по частотному спектру. Очевидно, что аналогичная функция может быть определена и для пульсации поперечной скорости u’2, указывающей на то, что размерность функции спектральной плотности равна м2 / С.

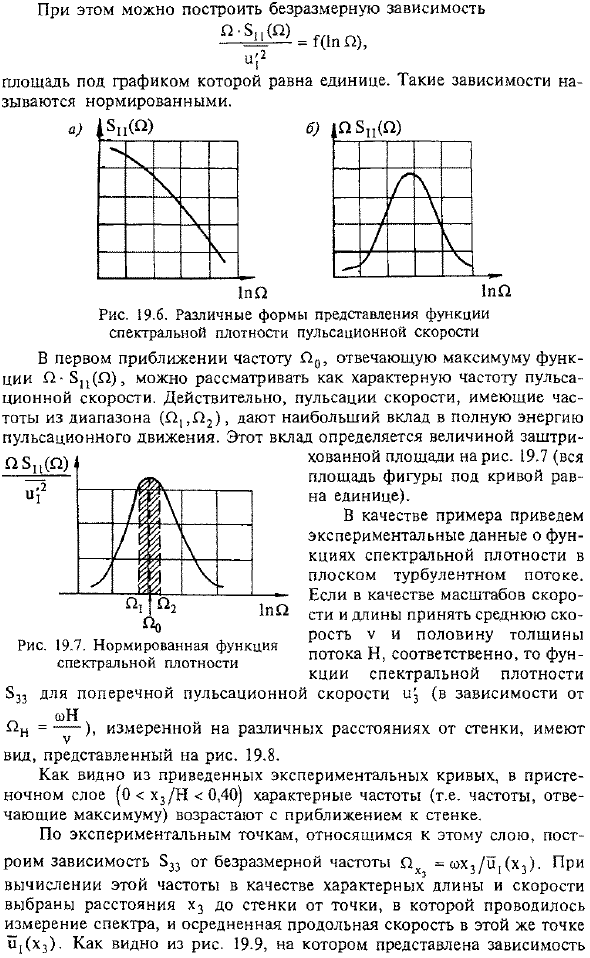
• Для более полного отражения распределения энергии в широком диапазоне частот функция спектральной плотности выражается в логарифмически построенной системе координат. Для этого необходимо сначала использовать соответствующую шкалу длины b и скорости, а затем перейти к безразмерной частоте 5p не может быть нормализовано, поэтому представление 1p (P) (рисунок 19.6, a), которое зависит от 5pp, несколько inconvenient. It невозможно выбрать такой масштаб для вертикальных координатных осей, чтобы площадь под графом Zi = $и (1пП) была равна 1.Отсутствие нормализации исключает возможность сравнения экспериментальных зависимостей, связанных с различными потоками, и получения универсальных функций, таких как спектральная плотность. Если по вертикальной оси откладывать не 5С (Р), А Р-5и (П), как это сделано на Рис. 5 19.6.6, то площадь под график зависимости от Р-5П (п)= г (1П П) равны.

Площадь под графом равна 1. Такая зависимость называется нормализацией. В первом приближении частота п8, соответствующая максимальному значению функции П −0 (П), П0, может рассматриваться как характерная частота пульсирующей скорости. Действительно, пульсации скорости с частотой в диапазоне (Р1; Р2) наиболее существенно вносят вклад в общую энергию пульсирующего движения. Этот вклад определяется величиной затененной части рисунка. 19.7 (вся площадь рисунка под кривой равна 1). В качестве примера приведены экспериментальные данные по спектральной функции плотности планарной турбулентности. Принимая половину средней скорости V и толщину потока H за шкалу скорости и длины соответственно, спектральную функцию плотности 833 (в зависимости от wH) поперечной пульсационной скорости u3).

При расчете этой частоты в качестве длины и скорости характеристики была выбрана средняя вертикальная скорость в той же точке, что и расстояние от точки измерения спектра до стенки. Людмила Фирмаль

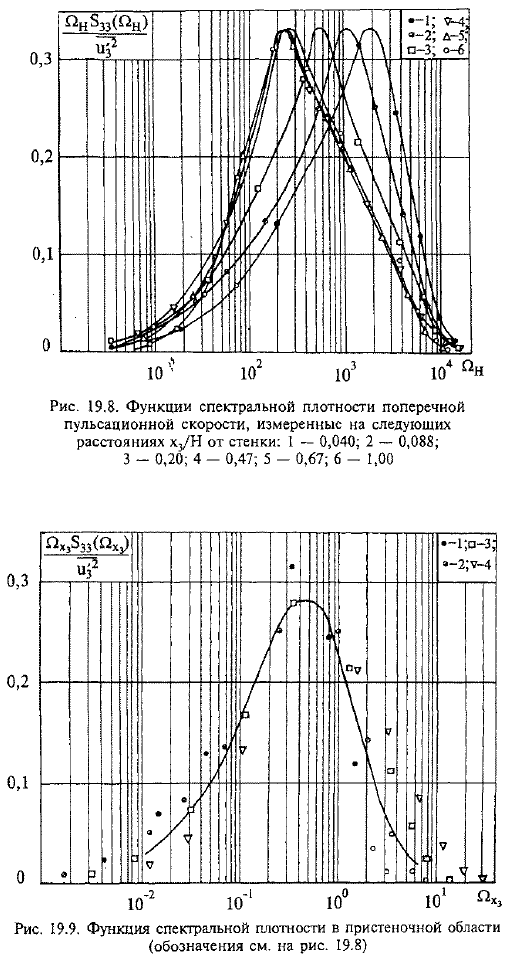
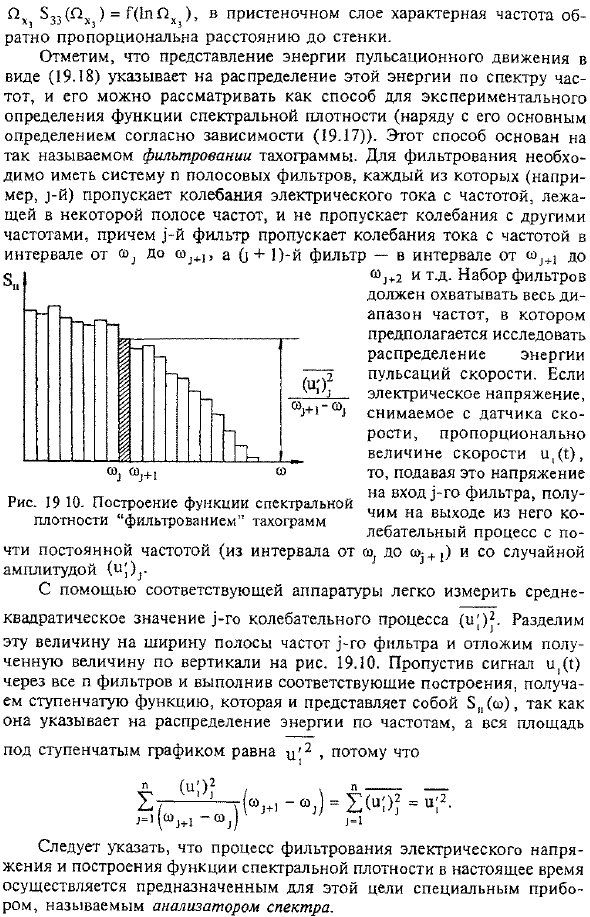
• Луна, измеренная на различных расстояниях от стены, имеет Фигура, показанная на фиг. 19.8. Как видно из экспериментальной кривой, при приближении слоя к стенке (0 Х3 / ч 0,40) характерная частота (то есть частота, соответствующая максимуму) возрастает по мере приближения к стенке. Используйте экспериментальные точки, связанные с этим слоем, чтобы построить зависимость от 833 безразмерной частоты Px-sokh3 / u, (x3).19.9, как видно из рисунка, показаны зависимости. Следует отметить, что выражение энергии пульсирующего движения в виде (19.18) показывает распределение этой энергии по всему частотному спектру и может рассматриваться как метод экспериментального определения функции спектральной плотности(с основным определением по зависимости(19.17)).Этот метод основан на так называемой фильтрации.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Полуэмпирические методы решения задач о свободной турбулентности.
2. Основные понятия статистической гидромеханики.
3. Задачи экспериментального изучения движения жидкостей.
4. Предпосылки использования анализа размерностей.