Оглавление:
Частные производные высших порядков
Рассмотрим функцию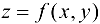 
. Если данная функция имеет в некоторой открытой области D частную производную по одной из переменных, то данная производная, сама являясь функцией от 
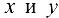, может в свою очередь в некоторой точке 
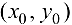иметь частную производную по той же или другой переменной. Для исходной функции частные производные 
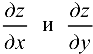называют частными производными первого порядка. Тогда, если первая производная была взята, например, по 
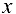, ее производные
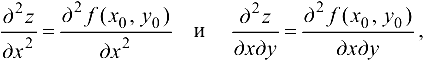
или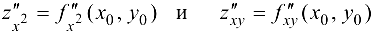 
называются частными производными второго порядка.
Аналогичным образом определяются частные производные третьего, четвертого и более высоких порядков.
Частная производная высшего порядка, взятая по различным переменным, например,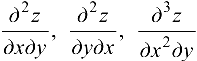 
, называется смешанной частной производной.
Пример 13.1.
Найти все частные производные второго порядка функции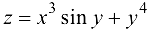 
.
Решение:
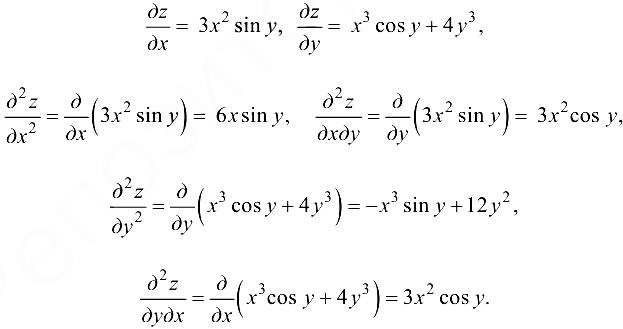
Ответ: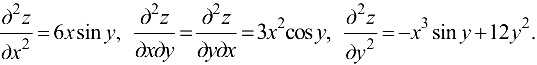 
Пример 13.2.
Найти все частные производные второго порядка функции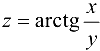 
.
Решение:
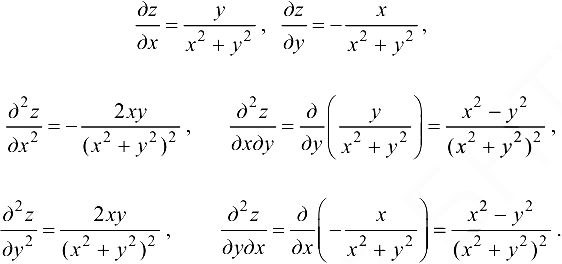
Ответ: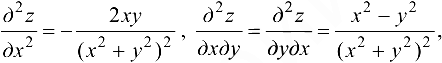 
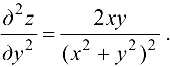
Заметим, что равенство смешанных производных не вытекает из самого определения смешанных производных. Существуют случаи, когда такого совпадения не наблюдается.
Теорема 13.1*. Пусть:
1) функция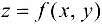 
определена в открытой области 
:
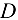2) в этой области существуют первые производные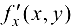 
и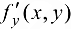 
3) в этой области существуют вторые смешанные производные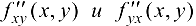 
, которые, как функции 
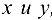, непрерывны в некоторой точке 
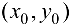области D.
Тогда в этой точке
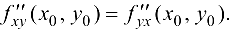
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
