Оглавление:




Цена как центральное поле кривых на плоскости
Цена как центр поля кривой на плоскости. Мы отступаем от идеологической стороны уравнения Макемама и пытаемся понять характеристики цены как функции зрелости n и доходности i.
- Это имеет больше смысла, потому что вы можете легко ответить на многие практические вопросы. Конечно, второй вариант предоставления кредита, в этом контексте,
использует более простой второй вариант, чтобы предоставить кредит первым. Людмила Фирмаль
Для этого учитываются соответствующие кривые на плоскости (r, a). a = D (n, α) = ND (1-α, $) + Cvn, (3.1) зависит от параметра n. Где это цена. Соответствует данным n и i. Кроме того, функция A (n,?) Является плоскостью i> 0, n> 0, точнее, счетным множеством луча 1 (r> 0, n = 1 / k), / = 0,1
Предположим, определено … первый координатный угол этой плоскости. Чтобы сделать это возможным, введите 1 kp 1 count = 0 как обычно. Если семейство в области определения 0 0 цена a = A (n, i) является убывающей функцией i для всех r> 0.
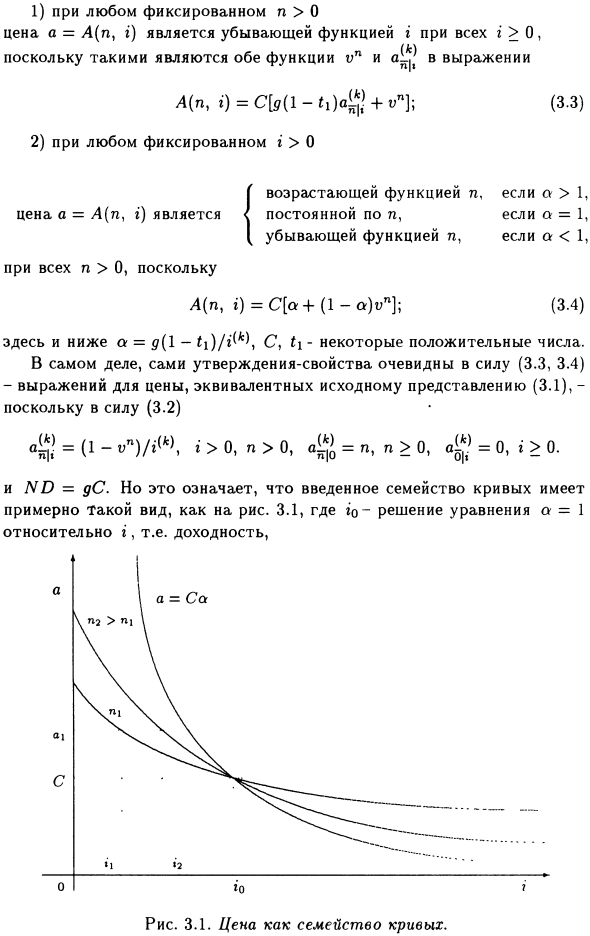
- Обе функции vn имеют формулу 4 (n, ») = C [s (l-tJaL ! + А»]; (3.3) 2) фиксированное i> 0, возрастающая функция n, a> 1, цена a = A (n, r) — убывающая функция n, a = 1, a <1, все n> 0, A (n, i) = C [a + (1-a) un]; (3.4) Вверх и вниз a = )> *> 0, n> 0, = n, n> 0, al * ‘= 0, i> 0. и ND = dC.
Введенная группа кривых имеет почти такой же формат, как на фиг. ‘o является решением уравнения o = 1, или прибыльности, для г.
Рисунок 3.1. Цена как набор кривых для o = 1. Людмила Фирмаль
Кстати, как видно из рисунка 3.1, 1) существует цепочка эквивалентных неравенств r < r0 <=> a> 1 <=> a> C (3.5) (a = A (n, r)> C> 0) и 2) все кривые в этом семействе a) 4 (0, r) = C, так что оно совершенно ясно при первом координатном угле плоскости (r, a)
Занимает площадь r> 0; b) A (oo, r) = Ca, r> 0; c) A (n, 0) = C [<7 (1-ti) n 4-1], n > 0, где A (oo, i) = limn-> oo A (n, r) или, точнее, вертикальная полоса, основание которой равно 0 C, r = 0 и кривая «гипотенузы» a = Сех.
Таким образом, для горизонтальной полосы 0 0 можно сказать, что семейство представляет собой нож, лезвие которого представляет собой прямую линию a = C. Замечания 3.1. Каждое из трех приведенных выше выражений имеет свое значение.
Первый (3.1) как бы описывает весь процесс выполнения обязанностей обеих сторон. Второе и третье (3.3) и (3.4) помогают достичь вышеуказанных свойств. Но есть и другая формула. A (n, r) = K4- (1-G) /, (3.6) где I = DNa ™ = gC (l-vn) / iw = a (C- / <) / (1- “,
Это то же самое для процентов, поскольку оно разбивает цену на два естественных условия: погашение всех 113 чистых процентов K и PZ (1-ti) I (т.е. инвестор с учетом оплаченного PN Получите; I-PP интереса, т. Е. Инвестором до уплаты PN) •
Примечания 3.2. Для малых i функция a = Ca параметра i, смежного с нижним правым семейством, почти гиперболическая На самом деле == A: [(14-i) 1 / * -1], поэтому «« [li (k-1) / 2Ai] и, следовательно, «# (1-ti) / i [ li (kl) / 2fc], r-> 0.
В случае r’o z = <(1- на основе уравнения i0 = [1, 4- 0, 2) 2) фиксированных r> 0 (£, a> 1 Число) константа 、, σ = 1, убывающая функция от t, a <1, точка nt = (ni 4-, •••, mn 4-t (3m) — прямая линия, то есть при увеличении параметра t) , Фиксированный> O, 52 ™ D> O-
Смотрите также:
| Другие подходы и бессрочные ренты. | Дата погашения принадлежит интервалу. |
| Влияние срока погашения на доходность. | Распределение момента погашения известно. |

