Задача №55.
Брус (рис. 3.16, а) шарнирно закреплен в точке 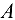 , а в точке
, а в точке 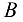 опирается па выступ стенки, образуя с горизонтальной плоскостью угол 30°. В точке
опирается па выступ стенки, образуя с горизонтальной плоскостью угол 30°. В точке 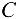 на расстоянии
на расстоянии 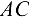 = 1 м брус нагружен перпендикулярной к нему силой
= 1 м брус нагружен перпендикулярной к нему силой 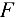 = 800 Н. Определить реакцию шарнира
= 800 Н. Определить реакцию шарнира 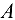 и выступа, если
и выступа, если 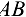 = 2,4 м.
= 2,4 м.
Решение:
Порядок решения этой задачи может быть следующим:
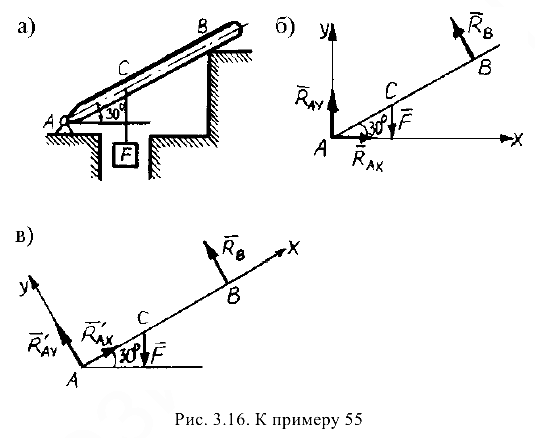
- Изобразим заданный груз вместе с нагрузками на рисунке, соблюдая при этом угол наклона бруса и масштаб для размеров по его длине (рис. 3.16, б).
- Освободим брус от связей (в точках
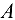 и
и 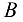 ), заменив эти связи их реакциями. Нужно помнить, что при свободном опирании тела о связь реакция связи направлена от связи к телу перпендикулярно либо поверхности тела, либо поверхности связи. В данном случае конец бруса
), заменив эти связи их реакциями. Нужно помнить, что при свободном опирании тела о связь реакция связи направлена от связи к телу перпендикулярно либо поверхности тела, либо поверхности связи. В данном случае конец бруса 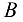 опирается на выступ стены, значит, реакция выступа направлена перпендикулярно брусу (рис. 3.16, б и 3.16, в). Направление реакции неподвижного шарнира
опирается на выступ стены, значит, реакция выступа направлена перпендикулярно брусу (рис. 3.16, б и 3.16, в). Направление реакции неподвижного шарнира 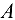 , как правило, заранее неизвестно, и поэтому эту реакцию заменяем ее составляющими, направленными вдоль выбранных координатных осей
, как правило, заранее неизвестно, и поэтому эту реакцию заменяем ее составляющими, направленными вдоль выбранных координатных осей 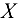 и
и 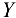 . Приняв за начало координат точку
. Приняв за начало координат точку 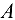 , можно придать осям обычное горизонтально-вертикальное положение (рис. 3.16, б), тогда реакция
, можно придать осям обычное горизонтально-вертикальное положение (рис. 3.16, б), тогда реакция 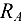 шарнира
шарнира 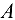 заменяется составляющими
заменяется составляющими 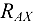 и
и 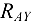 . Но можно выбрать иное направление осей, например: ось
. Но можно выбрать иное направление осей, например: ось 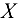 совместить с брусом
совместить с брусом 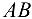 , а ось
, а ось 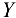 направить перпендикулярно брусу (рис. 3.16, в), тогда реакция шарнира
направить перпендикулярно брусу (рис. 3.16, в), тогда реакция шарнира 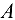 заменяется составляющими
заменяется составляющими 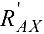 и
и 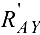
- Для получившейся расчетной схемы действия на брус плоской системы четырех сил составим три уравнения равновесия. Если задача решается по схеме на рис. 3.16, б, то целесообразно составить уравнения:
а) 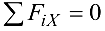 — алгебраическая сумма проекций всех сил па ось
— алгебраическая сумма проекций всех сил па ось 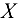 ;
;
б) 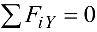 — алгебраическая сумма проекций всех сил на ось
— алгебраическая сумма проекций всех сил на ось 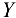 ;
;
в) 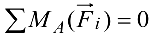 — алгебраическая сумма моментов всех сил относительно шарнира
— алгебраическая сумма моментов всех сил относительно шарнира 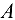 .
.
Если задача решается по схеме на рис. 3.16, в, то целесообразно составить уравнения:
а’)  — алгебраическая сумма проекций всех сил на ось
— алгебраическая сумма проекций всех сил на ось 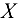 ;
;
б’) 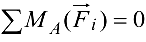 — алгебраическая сумма моментов всех сил относительно точки
— алгебраическая сумма моментов всех сил относительно точки 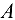 (неподвижного шарнира);
(неподвижного шарнира);
в’) 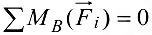 — алгебраическая сумма моментов всех сил относительно точки
— алгебраическая сумма моментов всех сил относительно точки 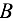 .
.
- Решить уравнения и найти численные значения сил
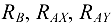 (или
(или 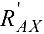 и
и 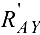 ).
). - Сложить по правилу параллелограмма составляющие
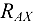 и
и 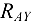
(или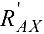 и
и 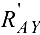 ) и найти численное значение
) и найти численное значение 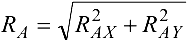 и направление вектора
и направление вектора 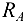 относительно бруса
относительно бруса 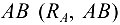 . Вектор
. Вектор 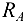 изобразить на рисунке.
изобразить на рисунке. - Проверить правильность решения задачи. В данном случае проверку решения следует выполнить, используя теорему о равенстве трех непараллельных сил, лежащих в одной плоскости: изобразить брус
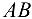 , точно соблюдая требования, содержащиеся в условии задачи, провести линии действия данной силы
, точно соблюдая требования, содержащиеся в условии задачи, провести линии действия данной силы 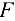 и найденной реакции
и найденной реакции 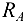 (эти линии пересекутся в какой-то точке
(эти линии пересекутся в какой-то точке 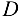 ). Если задача решена правильно, то линия действия реакции
). Если задача решена правильно, то линия действия реакции 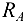 , проведенная под найденным углом
, проведенная под найденным углом 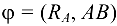 пройдет также через точку
пройдет также через точку 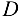 .
.
Для бруса, изображенного на рис. 3.16, а, решение выглядит так.
По схеме па рис. 3.16, б уравнения имеют вид
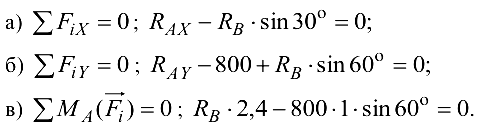
Из уравнения (в) получаем
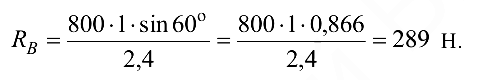
Из уравнения(а) получаем
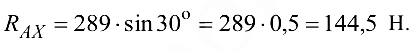
Из уравнения (б) получаем
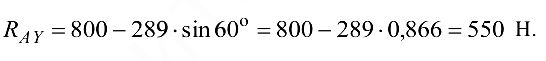
Численные значения 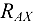 и
и 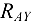 получились положительными, значит, они в действительности направлены так, как показано па рисунке, т. е.
получились положительными, значит, они в действительности направлены так, как показано па рисунке, т. е. 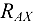 вправо вдоль оси
вправо вдоль оси 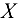 , a
, a 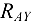 — вверх вдоль оси
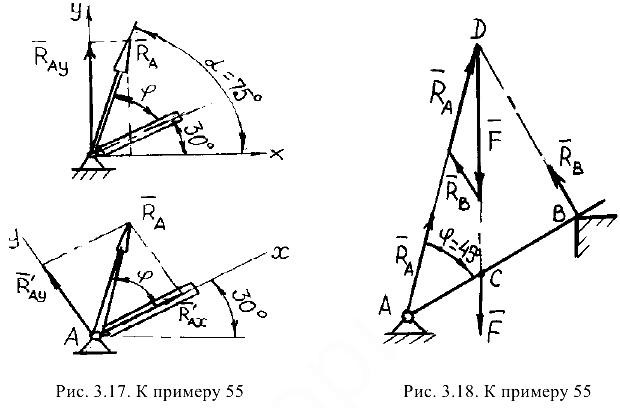
— вверх вдоль оси 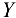 (рис. 3.17, а). Если бы какая-либо из составляющих получилась отрицательной, это означало бы, что она направлена в противоположную сторону относительно направления, указанного на рисунке.
(рис. 3.17, а). Если бы какая-либо из составляющих получилась отрицательной, это означало бы, что она направлена в противоположную сторону относительно направления, указанного на рисунке.
Определяем численное значение реакции шарнира 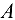 :
:
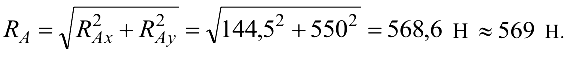
Определяем угол 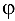 , образуемый вектором
, образуемый вектором 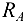 , с осью
, с осью 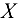 (рис. 3.17):
(рис. 3.17):
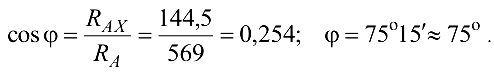
Таким образом угол
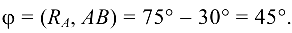
Решая задачу по схеме на рис. 3.16, в, получим такие уравнения:

Последовательно из уравнений (а’), (б’) и (в’) находим
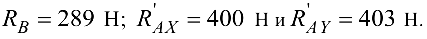
Значит, в этом случае направления составляющих 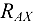 и
и 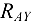 совпадают с положительным направлением осей (рис. 3.17, б). Численное значение реакции шарнира
совпадают с положительным направлением осей (рис. 3.17, б). Численное значение реакции шарнира 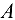
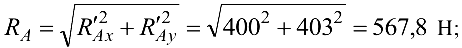
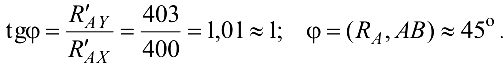
Как видим, результаты обоих решений полностью совпадают. Незначительные различия в ответах лежат в пределах, допустимых при подсчете. Проверив решение (см. п. 6), увидим (см. рис. 3.18), что линии действия трех сил 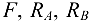 пересекаются в одной точке. Значит, задача решена правильно.
пересекаются в одной точке. Значит, задача решена правильно.
Ответ:
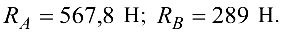
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

