Безотрывное обтекание цилиндра однородным потоком невязкой жидкости

Безотрывное обтекание цилиндра однородным потоком невязкой жидкости

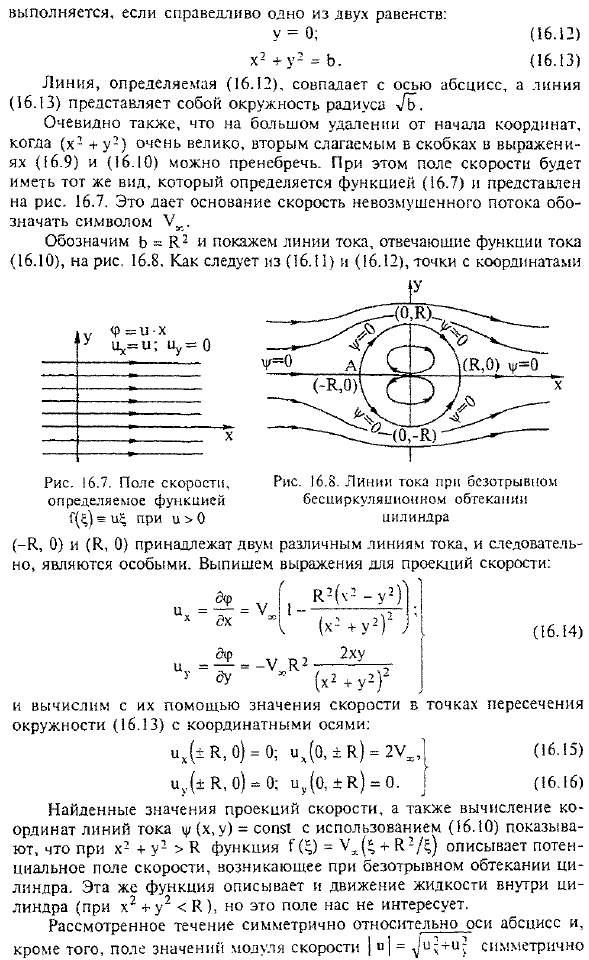
Безотрывное обтекание цилиндра однородным потоком невязкой жидкости. Рассмотрим решение задачи о потенциальном движении невязкой несжимаемой жидкости с использованием функции комплекса variable. As уже упоминалось в разделе. Невозможно заранее предсказать, какая функция [3.8, комплексная переменная c,-x + y]определяет то или иное поле скоростей. Например, функция Здесь и находится действительное число и определяется поле скоростей с потенциалом СР(х, г)=их, и=-=А = const и = !, и = = ^ = 0; ток линии Равенство φ (x, y)= uy =ω!Выглядит как горизонтальная линия(рис. 16.7).

Поэтому сначала следует рассмотреть некоторые из простейших функций и представить, что сумма функций и суперпозиция соответствующих потенциальных потоков описывают поле скорости объекта. Людмила Фирмаль

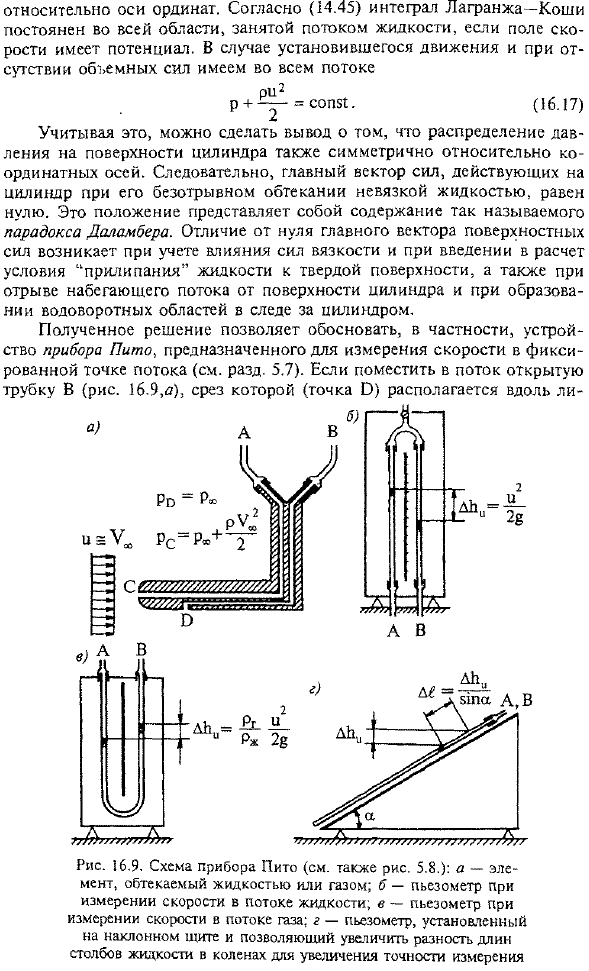
• Рассмотрим поле скорости, которое определяет функция Для этого представим Γ () в виде комплексной функции от 2 вещественных переменных x и Y. Найдем расположение линии потока φ (x, y)= 0. Это потенциал скорости. Если любое из двух равенств истинно. Линия, определенная в (16.12), совпадает с горизонтальной осью, а линия (16.13) представляет собой окружность с радиусом-L. Также понятно, что если (x + y2) очень большое, то на большом расстоянии от начала координат можно игнорировать 2-й член в скобках формулы (16-9) и (16.10). в этом случае поле скорости будет иметь одинаковое значение format. It определяется функцией (16.7) и показана на рисунке. 16.7.

Это дает основание для ненарушенной скорости потока, обозначенной символом\^. B-H2 обозначает линию потока, соответствующую функции потока на рисунке 16.8 (16.10). Точки с координатами, как следует из (16.11) и(16-12) Рис. 16.7.Поле скорости, определяемое функцией C (E.), равно > 0 (B, 0) и (K, 0) являются особыми, потому что они принадлежат к 2 различным линиям тока. Давайте напишем формулу для прогнозирования скорости. И с их помощью вычисляем значение скорости пересечения окружности (16.13)с координатными осями. Найденные значения проекции скорости и вычисление координат линий тока y (x, y)= co $ 1 с помощью(16.10) показывают, что для x2 + y2> K функция Γ (H.)= + H2/%) описывает потенциал Социальное поле скорости, которое возникает в непрерывном потоке вокруг цилиндра.

• Эта же функция также описывает движение жидкости в цилиндре, но это поле не интересует. Рассматриваемый поток симметричен относительно поля абсцисс и далее значения коэффициента скорости. 1 = симметричный Относительно оси ординат. Согласно (14.45), при наличии потенциала в поле скоростей Интеграл Лагранжа Коши постоянен на всей площади, занимаемой жидкостью flow. In случай устойчивого движения, если нет объемной силы, весь поток Это позволяет сделать вывод, что распределение давления на поверхности цилиндра также симметрично относительно координаты axes. As

Эта позиция составляет содержание так называемого парадокса Д’Аламбера. Разность между нулем основного вектора поверхностных сил учитывает действие вязких сил и условия «прикрепления» жидкости к твердой поверхности, а протекающий поток отделяется от поверхности цилиндра и возникает при образовании вихрей в постпроточной области цилиндра. Полученное решение позволяет продемонстрировать устройство прибора Пито, в частности, предназначенное для измерения скорости в неподвижной точке потока (см. раздел 5.7).

В результате основной вектор силы, действующей на цилиндр при непрерывном обтекании невязкой жидкости, равен нулю. Людмила Фирмаль

• Когда вы помещаете открытую трубку B в поток (рис. 16.9, а), ее срез (точка O) помещается вдоль обтекаемой линии, и жидкость в этой трубке помещается под потенциальным давлением H =(r + p / y ^если поток находится в шаре, скорость будет равна нулю, а согласно Бернулли (14.45 p), давление в (and2 / 2).Поэтому, когда вы соединяете открытую трубку а с отверстием в точке С, это давление уравновешивается водяным столбом. Второй Выше, чем трубка B. By измеряя уровень воды солнечного света в трубках а и в, можно рассчитать скорость и набегающий поток из (16.18).

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Силы, действующие на обтекаемое жидкостью тело.
2. Обтекание плоской пластины.
3. Присоединенный вихрь и подъемная сила.
4. Пограничный слой.