Оглавление:





Безмоментные оболочки вращении
- Мгновенное вращение оболочки. Общий случай плоского напряженного состояния почти точно реализуется в тонкой оболочке, куполе, баке и др. Если оболочка выпуклая, то можно показать, что существует полная или Гауссова кривизна 106 некоторые примеры расчета прочности[CHAP. IV Все точки положительны, и изгиб происходит только вблизи точки крепления, или толщина оболочки резко меняется.
В большинстве оболочек напряжение можно считать равномерно распределенным по толщине. Общая проблема равновесия тонкостенных оболочек является предметом теории упругости, которая достаточно сложна даже при игнорировании изгиба. Здесь мы рассмотрим наиболее важные случаи на практике, когда оболочка имеет форму вращающейся плоскости,
а нагрузка симметрична относительно оси. Людмила Фирмаль
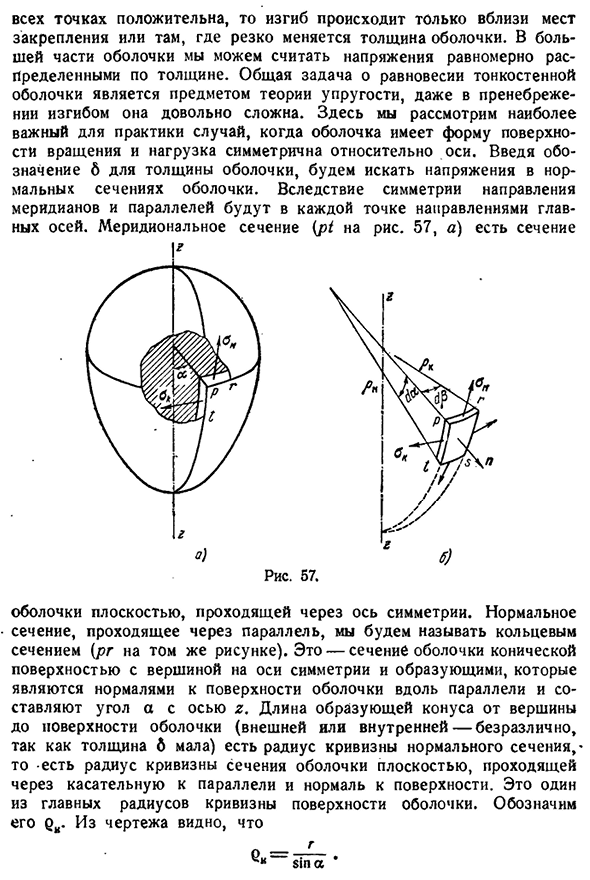
Найдите напряжения в нормальном сечении оболочки, введя обозначение толщины оболочки S. Из-за симметрии Меридиан и направление параллельной линии будут в направлении главной оси в каждой точке. Разница обусловлена частью{pt). 57, а) имеется раздел С плоскостью, проходящей через ось симметрии. Нормальное сечение, чтобы пройти через параллель, мы называем кольцевым сечением (показано на рисунке).
Это участок оболочки поверхности конуса с вершиной на оси симметрии, параллельной поверхности оболочки, а длина конуса от верхней грани оболочки, составляющая угол а к оси z (не радиус внешнего или внутреннего-толщина d мала), является радиусом нормального сечения этого одного из главных радиусов. Он представлен QB. Видно из рис.__г грехе§ 52] вращение одноступенчатыми оболочки 107 Эта сила-проекция Где r-расстояние от рассматриваемой точки поверхности до оси вращения.
- Давайте также покажем радиус кривизны Меридиана в Qm. К симметрии нагрузки в сечении Север-Юг, только нормальное напряжение, его Нормаль равна<tk6ds «cos(4+y)= — y STK d s» сила rs, действующая на грань, дает нормали точно такую же проекцию. Учитывая полностью подобный цикл, действующий на грани RG и st, проекция на каждую Нормаль выглядит следующим образом Наконец, внешняя силовая составляющая, направленная вдоль нормали, равна 4Д СК ДСК.
Если вы суммируете проекцию для всех нормалей силы, которые действуют на элемент, и уравняете эту сумму до нуля, вы получите AK6dsK dp+om6ds * da=q dsM ds*. Берегись этого. Окончательный (52.1) Окружной прокурор.- Дь См Форма уравнения равновесия выглядит следующим образом: H*_ / _ ®и=J — Дь кв. м б Из этого уравнения мы пренебрегли тем фактом, что области не
одинаковы, и тем фактом, что напряжения этих плоскостей при выводе плоскостей RG и ts обычно различны. Людмила Фирмаль
Это не нарушает правильности формулы (52.1), так как отброшенный член имеет значение выше 108 в некоторых примерах расчета прочности[гл. IV Порядок малости. Учитывая эти условия, можно составить уравнения равновесия с проекцией осей в плоскости, касательной к оболочке. В отличие от уравнений(52.1), они уже не конечны, а дифференциальны. Мы не будем вступать на этот путь, нормальный для теории упругости. Чтобы найти АК и АМ, нужно добавить еще одно уравнение к уравнению (52.1).
Мы получаем его, рассматривая равновесие частей оболочки, разрезанных вдоль конической поверхности кольцевого сечения. Площадь конусной поверхности сечения равна 2lgb, и если спроецировать ось всех сил и симметрично zz, то получим 2nrS<JMsina-Z-0. (52,2) где Z-сумма проекций на ось ZZ внешней силы, приложенной к разрезанной части оболочки.
Рассмотрим простейшие примеры применения этих уравнений. а)с Ф Е Р И Ч Е С К А я Б О Л О Ч К А П О Д Д Е Й с Т В и Е М Н у Т Р Е Н Ам=Ак для симметрии. Поскольку Qm=qk=q, мы получаем следующее уравнение из уравнения (52.1: ==(52.3) б)C i l I n d R I h E s K a I o l O h K a p O d d e y s t I m n u t R e n n e g o d a V l E N I. В этом случае Z-сила, действующая на Дио цилиндра: З=н р * и Q. Согласно формуле (52.2)) посетители я A » — радиус кривизны 2d Меридиана qm=oo, тогда как QK=r. уравнение (52.1) дает непосредственное кольцевое напряжение:
Хотите рассчитать прочность пластиковой цилиндрической оболочки, мы принимаем: _qr с QR-л °я=°к=т ’ <т.=ам=^,= Исходя из условий пластичности трески, расчет оболочки осуществляется по следующей формуле: — =Ч Ф Если мы примем ситуацию Мизеса, то получим: 109 § 53] о локальном напряжении в оболочке мембраны При равном запасе прочности толщина стенки, рассчитанная в соответствии с требованиями МЧС, на 14% меньше, чем при условии трески-Сен-Венана.
Смотрите также:
| Энергия изменения формы | Местные напряжения в безмоментных оболочках |
| Расчеты на прочность изделий сложной формы | Большие прогибы мембраны |

